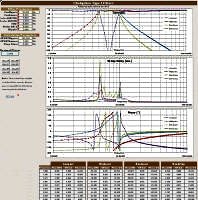
Chebyshev Filter Calculator in RF Cafe's
Espresso Engineering Workbook, created by Kirt Blattenberger, 2/2/2026.
For decades - literally - I searched in vain for explicit equations for calculating
Chebyshev filter phase and group delay, but could never find more than textbook
definitions, with instruction to extract phase from the real and imaginary parts
of the magnitude equation, and then take the negative first derivative of the phase
to get group delay. A lot of good that did - not! I have perused dozens of filter
design books, to no avail. Even the filter bible -
Zverev's Handbook
of Filter Synthesis - did not provide the needed equations. Most online resources
present Mathcad, MATLAB, Mathematica, or similar scripts that call the built-in
functions, without exposing the gory detail behind them. What I wanted was something
I could implement in a spreadsheet or a program.
Finally, with the help of AI (through many iterations of revisions to its mostly
erroneous results), I believe I have come up with equations which can be implemented
in relatively simple code. In fact, they now live in my
Espresso Engineering Workbook (free download). Lowpass, highpass, bandpass,
and bandstop filters are included. I checked the lowpass Chebyshev lowpass filter
(cutoff frequency of ω = 1 radian/second) group delay against the Zverev response
graphs for 0.01 dB and 0.1 dB passband ripple, and got excellent agreement.
Please let me know if you experience a problem.
Until people start copying and republishing my work, this is probably the only
place you will find this on the Internet. I had
Archive.org save a copy of this
page to prove my original work. You're welcome.
First, here is a simple explanation of how it works, then the full VBA code is
presented.
*******************************************************************************
This is a robust, self-contained Excel 2007 VBA suite of functions for analyzing analog
Chebyshev Type-I filters (ripple in the passband). It provides magnitude (dB),
phase (degrees), and group delay (seconds) for all four standard configurations
- lowpass, highpass, bandpass, and bandstop - without requiring any external
add-ins or worksheet function calls beyond basic math utilities.
Key Technical Features
- Classical Design: The code implements standard analog filter theory.
It calculates the ripple parameter ε from the passband ripple (r in dB),
distributes N poles on a Chebyshev ellipse in the left-half plane, and applies
frequency transformations to derive highpass, bandpass, and bandstop poles.
- Pole-Sum Method: For phase and group delay, the functions sum contributions
from each individual pole (vector geometry). Group delay uses the formula
–Re(pole)/|jω – pole|², while phase uses the angle of the vector from the pole
to the imaginary axis.
- Complex Arithmetic: Bandpass and bandstop transformations require solving
quadratics with complex coefficients. An inlined a complex square-root
algorithm (algebraic method) to keep the code self-contained and fast.
- Numerical Stability: The bandstop magnitude calculation works in the
log-domain (summing log-distances to poles/zeros) to prevent floating-point
overflow with high-order filters. Phase results are wrapped to the ±180° range.
- Excel Optimization: All loops use scalar Double variables (no slow array
allocation), and constants (π, ln 10) are hard-coded to avoid repeated lookups. The later functions avoid
WorksheetFunction calls entirely, improving recalculation speed.
*******************************************************************************
'======================================================================
' FULL SELF-CONTAINED CHEBYSHEV TYPE-I FILTER SUITE (Hz inputs)
' GD(sec)/PH(deg)/Mag(dB)
for LP/HP/BP/BS. NO EXTERNAL CALLS. MAX SPEED.
' Inline CSqrt (alg), ChebyT (recursive).
Analytical Mag (fastest/exact).
' Pole-sum GD/PH (unavoidable).
Copyright Kirt Blattenberger February 2026
'=======================================================================
'===============================================================================
' INLINE CSQRT (ALG): Used only in BP/BS GD/PH (copied per func for no calls)
'===============================================================================
' Private helper not needed: duplicated inline.
'************************************
'******** CHEBYSHEV LOWPASS ********
'************************************
Function ChebyLPGroupDelay(f As Double, fCo As Double, r As Double, N As Integer)
As Double
Const PI As Double = 3.14159265358979
Const TWOPI As Double = 6.28318530717959
Dim epsilon As Double, omega As Double, OmegaCo As Double
Dim s As Double, theta
As Double, sinh_val As Double, cosh_val As Double
Dim alpha As Double, beta As
Double, pole_real As Double, pole_imag As Double
Dim numer As Double, denom As
Double, GD_sum As Double, k As Integer
If fCo <= 0 Or N <= 0 Or r <=
0 Then ChebyLPGroupDelay = 0: Exit Function
OmegaCo = TWOPI * fCo: omega = TWOPI
* f
epsilon = Sqr(10 ^ (r / 10) - 1)
s = Application.WorksheetFunction.Asinh(1
/ epsilon) / N
sinh_val = Application.WorksheetFunction.Sinh(s): cosh_val = Application.WorksheetFunction.Cosh(s)
GD_sum = 0
For k = 1 To N
theta = PI * (2 * k - 1) / (2 * N)
alpha = -sinh_val
* Sin(theta): beta = cosh_val * Cos(theta)
pole_real = alpha * OmegaCo: pole_imag
= beta * OmegaCo
numer = pole_real: denom = pole_real ^ 2 + (omega - pole_imag)
^ 2
GD_sum = GD_sum + numer / denom
Next k
ChebyLPGroupDelay = -GD_sum
End Function
Function ChebyLPPhase(f As Double, fCo As Double, r As Double,
N As Integer) As Double
Const PI As Double = 3.14159265358979
Const TWOPI
As Double = 6.28318530717959
Dim epsilon As Double, omega As Double, OmegaCo
As Double
Dim s As Double, theta As Double, sinh_val As Double, cosh_val As Double
Dim alpha As Double, beta As Double, pole_real As Double, pole_imag As Double
Dim phase_sum As Double, angle_k As Double, k As Integer
If fCo <= 0 Or N <=
0 Or r <= 0 Then ChebyLPPhase = 0: Exit Function
OmegaCo = TWOPI * fCo: omega
= TWOPI * f
epsilon = Sqr(10 ^ (r / 10) - 1)
s = Application.WorksheetFunction.Asinh(1
/ epsilon) / N
sinh_val = Application.WorksheetFunction.Sinh(s): cosh_val = Application.WorksheetFunction.Cosh(s)
phase_sum = 0
For k = 1 To N
theta = PI * (2 * k - 1) / (2 * N)
alpha =
-sinh_val * Sin(theta): beta = cosh_val * Cos(theta)
pole_real = alpha * OmegaCo:
pole_imag = beta * OmegaCo
angle_k = Application.WorksheetFunction.Atan2((omega
- pole_imag), -pole_real)
phase_sum = phase_sum + angle_k
Next k
ChebyLPPhase
= -phase_sum * 180 / PI
Do While ChebyLPPhase > 180: ChebyLPPhase = ChebyLPPhase
- 360: Loop
Do While ChebyLPPhase < -180: ChebyLPPhase = ChebyLPPhase + 360:
Loop
End Function
Function ChebyLPMag(f As Double, fCo As Double, r As
Double, N As Integer) As Double
Const LN10 As Double = 2.30258509299405: Const
TWOPI As Double = 6.28318530717959
Dim epsilon As Double, zeta As Double, arg
As Double, omega As Double, OmegaCo As Double
Dim T0 As Double, T1 As Double,
Tn As Double, i As Integer
If fCo <= 0 Or N <= 0 Or r <= 0 Then ChebyLPMag
= 0: Exit Function
OmegaCo = TWOPI * fCo: omega = TWOPI * f
epsilon = Sqr(10
^ (r / 10) - 1): zeta = omega / OmegaCo
If N = 0 Then arg = 1#: GoTo MagLog
If N = 1 Then Tn = zeta: GoTo MagLog
T0 = 1#: T1 = zeta
For i = 2 To N
Tn = 2# * zeta * T1 - T0: T0 = T1: T1 = Tn
Next i
MagLog:
arg = 1# + epsilon
* epsilon * Tn * Tn
ChebyLPMag = -10# * Log(arg) / LN10
End Function
'************************************
'******** CHEBYSHEV HIGHPASS ********
'************************************
Function ChebyHPGroupDelay(f As Double,
fCo As Double, r As Double, N As Integer) As Double
Const PI As Double = 3.14159265358979:
Const TWOPI As Double = 6.28318530717959
Dim epsilon As Double, omega As Double,
OmegaCo As Double
Dim s As Double, theta As Double, sinh_val As Double, cosh_val
As Double
Dim alpha As Double, beta As Double, mag2 As Double
Dim pole_real
As Double, pole_imag As Double, numer As Double, denom As Double, GD_sum As Double,
k As Integer
If fCo <= 0 Or N <= 0 Or r <= 0 Then ChebyHPGroupDelay
= 0: Exit Function
OmegaCo = TWOPI * fCo: omega = TWOPI * f
epsilon = Sqr(10
^ (r / 10) - 1)
s = Application.WorksheetFunction.Asinh(1 / epsilon) / N
sinh_val
= Application.WorksheetFunction.Sinh(s): cosh_val = Application.WorksheetFunction.Cosh(s)
GD_sum = 0
For k = 1 To N
theta = PI * (2 * k - 1) / (2 * N)
alpha = -sinh_val
* Sin(theta): beta = cosh_val * Cos(theta)
mag2 = alpha * alpha + beta * beta
pole_real = OmegaCo * alpha / mag2: pole_imag = OmegaCo * (-beta) / mag2
numer
= pole_real: denom = pole_real ^ 2 + (omega - pole_imag) ^ 2
GD_sum = GD_sum
+ numer / denom
Next k
ChebyHPGroupDelay = -GD_sum
End Function
Function ChebyHPPhase(f As Double, fCo As Double, r As Double, N As Integer) As
Double
Const PI As Double = 3.14159265358979: Const TWOPI As Double = 6.28318530717959
Dim epsilon As Double, omega As Double, OmegaCo As Double
Dim s As Double, theta
As Double, sinh_val As Double, cosh_val As Double
Dim alpha As Double, beta As
Double, mag2 As Double
Dim pole_real As Double, pole_imag As Double, phase_sum
As Double, angle_k As Double, k As Integer
If fCo <= 0 Or N <= 0 Or r <=
0 Then ChebyHPPhase = 0: Exit Function
OmegaCo = TWOPI * fCo: omega = TWOPI *
f
epsilon = Sqr(10 ^ (r / 10) - 1)
s = Application.WorksheetFunction.Asinh(1
/ epsilon) / N
sinh_val = Application.WorksheetFunction.Sinh(s): cosh_val = Application.WorksheetFunction.Cosh(s)
phase_sum = 0
For k = 1 To N
theta = PI * (2 * k - 1) / (2 * N)
alpha =
-sinh_val * Sin(theta): beta = cosh_val * Cos(theta)
mag2 = alpha * alpha + beta
* beta
pole_real = OmegaCo * alpha / mag2: pole_imag = OmegaCo * (-beta) / mag2
angle_k = Application.WorksheetFunction.Atan2((omega - pole_imag), -pole_real)
phase_sum = phase_sum + angle_k
Next k
ChebyHPPhase = -phase_sum * 180 / PI
Do While ChebyHPPhase > 180: ChebyHPPhase = ChebyHPPhase - 360: Loop
Do While
ChebyHPPhase < -180: ChebyHPPhase = ChebyHPPhase + 360: Loop
End Function
Function ChebyHPMag(f As Double, fCo As Double, r As Double, N As Integer) As
Double
Const LN10 As Double = 2.30258509299405: Const TWOPI As Double = 6.28318530717959
Dim epsilon As Double, zeta As Double, arg As Double, omega As Double, OmegaCo As
Double
Dim T0 As Double, T1 As Double, Tn As Double, i As Integer
If fCo <=
0 Or N <= 0 Or r <= 0 Then ChebyHPMag = 0: Exit Function
OmegaCo = TWOPI
* fCo: omega = TWOPI * f
If omega = 0 Then ChebyHPMag = -200: Exit Function
epsilon = Sqr(10 ^ (r / 10) - 1): zeta = OmegaCo / omega
If N = 0 Then arg =
1#: GoTo MagLogHP
If N = 1 Then Tn = zeta: GoTo MagLogHP
T0 = 1#: T1 = zeta
For i = 2 To N
Tn = 2# * zeta * T1 - T0: T0 = T1: T1 = Tn
Next i
MagLogHP:
arg = 1# + epsilon * epsilon * Tn * Tn
ChebyHPMag = -10# * Log(arg) / LN10
End Function
'************************************
'******** CHEBYSHEV
BANDPASS ********
'************************************
Function ChebyBPMag(f
As Double, fL As Double, fU As Double, r As Double, N As Integer) As Double
Const
LN10 As Double = 2.30258509299405: Const TWOPI As Double = 6.28318530717959
Dim
epsilon As Double, zeta As Double, arg As Double, omega As Double, OmegaL As Double,
OmegaU As Double, w0 As Double, BW As Double
Dim T0 As Double, T1 As Double,
Tn As Double, i As Integer
If fL <= 0 Or fU <= fL Or N <= 0 Or r <=
0 Then ChebyBPMag = 0: Exit Function
OmegaL = TWOPI * fL: OmegaU = TWOPI * fU:
omega = TWOPI * f
If omega = 0 Then ChebyBPMag = -200: Exit Function
w0 =
Sqr(OmegaL * OmegaU): BW = OmegaU - OmegaL
epsilon = Sqr(10 ^ (r / 10) - 1):
zeta = (omega * omega - w0 * w0) / (BW * omega)
If N = 0 Then arg = 1#: GoTo
BPMagLog
If N = 1 Then Tn = zeta: GoTo BPMagLog
T0 = 1#: T1 = zeta
For
i = 2 To N
Tn = 2# * zeta * T1 - T0: T0 = T1: T1 = Tn
Next i
BPMagLog:
arg = 1# + epsilon * epsilon * Tn * Tn
ChebyBPMag = -10# * Log(arg) / LN10
End Function
Function ChebyBPGroupDelay(f As Double, fL As Double, fU As
Double, r As Double, N As Integer) As Double
Const PI As Double = 3.14159265358979:
Const TWOPI As Double = 6.28318530717959
Dim epsilon As Double, omega As Double,
OmegaL As Double, OmegaU As Double, w0 As Double, BW As Double
Dim lp_s As Double,
theta As Double, sinh_val As Double, cosh_val As Double
Dim alpha As Double,
beta As Double, gamma_re As Double, gamma_im As Double
Dim delta_re As Double,
delta_im As Double, mag As Double, sqrt_re As Double, sqrt_im As Double
Dim p1_re
As Double, p1_im As Double, p2_re As Double, p2_im As Double
Dim GD_contrib As
Double, GD_sum As Double, k As Integer
If fL <= 0 Or fU <= fL Or N <=
0 Or r <= 0 Then ChebyBPGroupDelay = 0: Exit Function
OmegaL = TWOPI * fL:
OmegaU = TWOPI * fU: omega = TWOPI * f
w0 = Sqr(OmegaL * OmegaU): BW = OmegaU
- OmegaL
epsilon = Sqr(10 ^ (r / 10) - 1)
lp_s = Application.WorksheetFunction.Asinh(1
/ epsilon) / N
sinh_val = Application.WorksheetFunction.Sinh(lp_s): cosh_val
= Application.WorksheetFunction.Cosh(lp_s)
GD_sum = 0
For k = 1 To N
theta
= PI * (2 * k - 1) / (2 * N)
alpha = -sinh_val * Sin(theta): beta = cosh_val
* Cos(theta)
gamma_re = BW * alpha: gamma_im = BW * beta
delta_re = gamma_re
* gamma_re - gamma_im * gamma_im - 4 * w0 * w0
delta_im = 2 * gamma_re * gamma_im
' INLINE CSQRT: principal Re>=0
mag = Sqr(delta_re * delta_re + delta_im *
delta_im)
If mag = 0 Then
sqrt_re = 0
sqrt_im = 0
Else
sqrt_re =
Sqr((mag + delta_re) / 2)
If delta_im < 0 Then
sqrt_im = -Sqr((mag - delta_re)
/ 2)
Else
sqrt_im = Sqr((mag - delta_re) / 2)
End If
End If
p1_re
= (gamma_re + sqrt_re) / 2: p1_im = (gamma_im + sqrt_im) / 2
p2_re = (gamma_re
- sqrt_re) / 2: p2_im = (gamma_im - sqrt_im) / 2
If p1_re >= 0 Or p2_re >=
0 Then
sqrt_re = -sqrt_re: sqrt_im = -sqrt_im
p1_re = (gamma_re + sqrt_re)
/ 2: p1_im = (gamma_im + sqrt_im) / 2
p2_re = (gamma_re - sqrt_re) / 2: p2_im
= (gamma_im - sqrt_im) / 2
End If
GD_contrib = p1_re / (p1_re * p1_re + (omega
- p1_im) ^ 2): GD_sum = GD_sum + GD_contrib
GD_contrib = p2_re / (p2_re * p2_re
+ (omega - p2_im) ^ 2): GD_sum = GD_sum + GD_contrib
Next k
ChebyBPGroupDelay
= -GD_sum
End Function
Function ChebyBPPhase(f As Double, fL As Double,
fU As Double, r As Double, N As Integer) As Double
Const PI As Double = 3.14159265358979:
Const TWOPI As Double = 6.28318530717959
Dim epsilon As Double, omega As Double,
OmegaL As Double, OmegaU As Double, w0 As Double, BW As Double
Dim lp_s As Double,
theta As Double, sinh_val As Double, cosh_val As Double
Dim alpha As Double,
beta As Double, gamma_re As Double, gamma_im As Double
Dim delta_re As Double,
delta_im As Double, mag As Double, sqrt_re As Double, sqrt_im As Double
Dim p1_re
As Double, p1_im As Double, p2_re As Double, p2_im As Double
Dim phase_sum As
Double, angle_k As Double, k As Integer
If fL <= 0 Or fU <= fL Or N <=
0 Or r <= 0 Then ChebyBPPhase = 0: Exit Function
OmegaL = TWOPI * fL: OmegaU
= TWOPI * fU: omega = TWOPI * f
w0 = Sqr(OmegaL * OmegaU): BW = OmegaU - OmegaL
epsilon = Sqr(10 ^ (r / 10) - 1)
lp_s = Application.WorksheetFunction.Asinh(1
/ epsilon) / N
sinh_val = Application.WorksheetFunction.Sinh(lp_s): cosh_val
= Application.WorksheetFunction.Cosh(lp_s)
phase_sum = 0
For k = 1 To N
theta = PI * (2 * k - 1) / (2 * N)
alpha = -sinh_val * Sin(theta): beta = cosh_val
* Cos(theta)
gamma_re = BW * alpha: gamma_im = BW * beta
delta_re = gamma_re
* gamma_re - gamma_im * gamma_im - 4 * w0 * w0
delta_im = 2 * gamma_re * gamma_im
mag = Sqr(delta_re * delta_re + delta_im * delta_im)
If mag = 0 Then
sqrt_re
= 0
sqrt_im = 0
Else
sqrt_re = Sqr((mag + delta_re) / 2)
If delta_im <
0 Then
sqrt_im = -Sqr((mag - delta_re) / 2)
Else
sqrt_im = Sqr((mag - delta_re)
/ 2)
End If
End If
p1_re = (gamma_re + sqrt_re) / 2: p1_im = (gamma_im
+ sqrt_im) / 2
p2_re = (gamma_re - sqrt_re) / 2: p2_im = (gamma_im - sqrt_im)
/ 2
If p1_re >= 0 Or p2_re >= 0 Then
sqrt_re = -sqrt_re: sqrt_im = -sqrt_im
p1_re = (gamma_re + sqrt_re) / 2: p1_im = (gamma_im + sqrt_im) / 2
p2_re = (gamma_re
- sqrt_re) / 2: p2_im = (gamma_im - sqrt_im) / 2
End If
angle_k = Application.WorksheetFunction.Atan2((omega
- p1_im), -p1_re): phase_sum = phase_sum + angle_k
angle_k = Application.WorksheetFunction.Atan2((omega
- p2_im), -p2_re): phase_sum = phase_sum + angle_k
Next k
ChebyBPPhase = -phase_sum
* 180 / PI
Do While ChebyBPPhase > 180: ChebyBPPhase = ChebyBPPhase - 360:
Loop
Do While ChebyBPPhase < -180: ChebyBPPhase = ChebyBPPhase + 360: Loop
End Function
'************************************
'******** CHEBYSHEV
BANDSTOP ********
'************************************
Function ChebyBSMag(f
As Double, fL As Double, fU As Double, r As Double, N As Integer) As Double
'===============================================================================
' ChebyBSMag - Chebyshev Bandstop Magnitude |H(j2pf)| in dB
' Self-contained:
no external helper / WorksheetFunction calls.
'===============================================================================
Const PI As Double = 3.14159265358979
Const TWOPI As Double = 6.28318530717959
Const LN10 As Double = 2.30258509299405
Dim epsilon As Double
Dim omega
As Double, OmegaL As Double, OmegaU As Double, w0 As Double, BW As Double
Dim
lp_s As Double, theta As Double, sinh_val As Double, cosh_val As Double
Dim alpha
As Double, beta As Double, qmag2 As Double
Dim gamma_re As Double, gamma_im As
Double
Dim delta_re As Double, delta_im As Double
Dim sqrt_re As Double, sqrt_im
As Double
Dim mag As Double
Dim p1_re As Double, p1_im As Double, p2_re As
Double, p2_im As Double
Dim log_num_sum As Double, log_den_sum As Double
Dim
dist_sq As Double, zero_mag As Double
Dim tmp As Double
Dim k As Integer
If fL <= 0 Or fU <= fL Or N <= 0 Or r <= 0 Then
ChebyBSMag =
0
Exit Function
End If
On Error GoTo ErrorHandler
OmegaL = TWOPI
* fL
OmegaU = TWOPI * fU
omega = TWOPI * f
w0 = Sqr(OmegaL * OmegaU)
BW = OmegaU - OmegaL
epsilon = Sqr(10 ^ (r / 10) - 1)
' lp_s = asinh(1/epsilon)
/ N
tmp = 1# / epsilon
lp_s = Log(tmp + Sqr(tmp * tmp + 1#)) / N
'
sinh(lp_s), cosh(lp_s)
tmp = Exp(lp_s)
sinh_val = 0.5 * (tmp - 1# / tmp)
cosh_val = 0.5 * (tmp + 1# / tmp)
' num: |w0^2 - Omega^2|^N => use logs
zero_mag = Abs(w0 * w0 - omega * omega)
If zero_mag <= 1E-300 Then
ChebyBSMag
= -1E+99
Exit Function
End If
log_num_sum = N * 0.5 * Log(zero_mag * zero_mag)
log_den_sum = 0#
For k = 1 To N
theta = PI * (2# * k - 1#) / (2# *
N)
alpha = -sinh_val * Sin(theta)
beta = cosh_val * Cos(theta)
qmag2
= alpha * alpha + beta * beta
gamma_re = BW * alpha / qmag2
gamma_im = BW
* (-beta) / qmag2
delta_re = gamma_re * gamma_re - gamma_im * gamma_im -
4# * w0 * w0
delta_im = 2# * gamma_re * gamma_im
' Complex sqrt of delta
(improved for real/near-real cases)
If Abs(delta_im) < 0.00000000000001 *
(Abs(delta_re) + 1#) Then ' Treat as real
If delta_re >= 0# Then
sqrt_re
= Sqr(delta_re)
sqrt_im = 0#
Else
sqrt_re = 0#
sqrt_im = Sqr(-delta_re)
End If
Else
mag = Sqr(delta_re * delta_re + delta_im * delta_im)
If mag
= 0# Then
sqrt_re = 0#
sqrt_im = 0#
Else
sqrt_re = Sqr((mag + delta_re)
/ 2#)
If delta_im >= 0# Then
sqrt_im = Sqr((mag - delta_re) / 2#)
Else
sqrt_im = -Sqr((mag - delta_re) / 2#)
End If
End If
End If
p1_re
= (gamma_re + sqrt_re) / 2#
p1_im = (gamma_im + sqrt_im) / 2#
p2_re = (gamma_re
- sqrt_re) / 2#
p2_im = (gamma_im - sqrt_im) / 2#
' Enforce LHP poles
If p1_re >= 0# Or p2_re >= 0# Then
sqrt_re = -sqrt_re
sqrt_im = -sqrt_im
p1_re = (gamma_re + sqrt_re) / 2#
p1_im = (gamma_im + sqrt_im) / 2#
p2_re
= (gamma_re - sqrt_re) / 2#
p2_im = (gamma_im - sqrt_im) / 2#
End If
dist_sq = (-p1_re) * (-p1_re) + (omega - p1_im) * (omega - p1_im)
log_den_sum
= log_den_sum + 0.5 * Log(dist_sq)
dist_sq = (-p2_re) * (-p2_re) + (omega
- p2_im) * (omega - p2_im)
log_den_sum = log_den_sum + 0.5 * Log(dist_sq)
Next k
ChebyBSMag = 20# * (log_num_sum - log_den_sum) / LN10
Exit Function
ErrorHandler:
ChebyBSMag = 0
End Function
Function ChebyBSGroupDelay(f
As Double, fL As Double, fU As Double, r As Double, N As Integer) As Double
'===============================================================================
' ChebyBSGroupDelay - Chebyshev Bandstop Group Delay (Hz inputs: f, fL, fU in Hertz)
' Self-contained: no external helper / WorksheetFunction calls.
'===============================================================================
Const PI As Double = 3.14159265358979
Const TWOPI As Double = 6.28318530717959
Dim epsilon As Double
Dim omega As Double
Dim OmegaL As Double, OmegaU
As Double
Dim w0 As Double
Dim BW As Double
Dim lp_s As Double
Dim theta
As Double
Dim sinh_val As Double
Dim cosh_val As Double
Dim alpha As Double,
beta As Double ' q_lp = alpha + j beta
Dim qmag2 As Double
Dim gamma_re As
Double, gamma_im As Double
Dim delta_re As Double, delta_im As Double
Dim
sqrt_re As Double, sqrt_im As Double
Dim mag As Double
Dim p1_re As Double,
p1_im As Double
Dim p2_re As Double, p2_im As Double
Dim GD_contrib As Double
Dim GD_sum As Double
Dim tmp As Double
Dim k As Integer
If fL <=
0 Or fU <= fL Or N <= 0 Or r <= 0 Then
ChebyBSGroupDelay = 0
Exit
Function
End If
On Error GoTo ErrorHandler
' Convert Hz to rad/s
OmegaL = TWOPI * fL
OmegaU = TWOPI * fU
omega = TWOPI * f
epsilon =
Sqr(10 ^ (r / 10) - 1)
w0 = Sqr(OmegaL * OmegaU)
BW = OmegaU - OmegaL
' lp_s = asinh(1/epsilon) / N
tmp = 1# / epsilon
lp_s = Log(tmp + Sqr(tmp
* tmp + 1#)) / N
' sinh(lp_s), cosh(lp_s)
tmp = Exp(lp_s)
sinh_val
= 0.5 * (tmp - 1# / tmp)
cosh_val = 0.5 * (tmp + 1# / tmp)
GD_sum = 0#
For k = 1 To N
theta = PI * (2# * k - 1#) / (2# * N)
alpha = -sinh_val
* Sin(theta)
beta = cosh_val * Cos(theta)
qmag2 = alpha * alpha + beta
* beta
gamma_re = BW * alpha / qmag2
gamma_im = BW * (-beta) / qmag2 ' 1/q
= conj(q)/|q|^2
' delta = gamma^2 - 4 w0^2 (complex)
delta_re = gamma_re
* gamma_re - gamma_im * gamma_im - 4# * w0 * w0
delta_im = 2# * gamma_re * gamma_im
' Complex sqrt of delta (principal branch, Re >= 0)
mag = Sqr(delta_re
* delta_re + delta_im * delta_im)
If mag = 0# Then
sqrt_re = 0#
sqrt_im
= 0#
Else
sqrt_re = Sqr((mag + delta_re) / 2#)
If delta_im > 0# Then
sqrt_im = Sqr((mag - delta_re) / 2#)
ElseIf delta_im < 0# Then
sqrt_im
= -Sqr((mag - delta_re) / 2#)
Else
sqrt_im = 0#
End If
End If
' Roots: [gamma +/- sqrt(delta)] / 2
p1_re = (gamma_re + sqrt_re) / 2#
p1_im = (gamma_im + sqrt_im) / 2#
p2_re = (gamma_re - sqrt_re) / 2#
p2_im
= (gamma_im - sqrt_im) / 2#
' Ensure LHP poles (flip sqrt branch if needed)
If p1_re >= 0# Or p2_re >= 0# Then
sqrt_re = -sqrt_re
sqrt_im = -sqrt_im
p1_re = (gamma_re + sqrt_re) / 2#
p1_im = (gamma_im + sqrt_im) / 2#
p2_re
= (gamma_re - sqrt_re) / 2#
p2_im = (gamma_im - sqrt_im) / 2#
End If
' GD from p1
GD_contrib = p1_re / (p1_re * p1_re + (omega - p1_im) * (omega
- p1_im))
GD_sum = GD_sum + GD_contrib
' GD from p2
GD_contrib = p2_re
/ (p2_re * p2_re + (omega - p2_im) * (omega - p2_im))
GD_sum = GD_sum + GD_contrib
Next k
ChebyBSGroupDelay = -GD_sum
Exit Function
ErrorHandler:
ChebyBSGroupDelay = 0
End Function
Function ChebyBSPhase(f As Double,
fL As Double, fU As Double, r As Double, N As Integer) As Double
'===============================================================================
' ChebyBSPhase - Chebyshev Bandstop Phase (poles only, degrees)
' Self-contained:
no external helper / WorksheetFunction calls.
'===============================================================================
Const PI As Double = 3.14159265358979
Const TWOPI As Double = 6.28318530717959
Dim epsilon As Double
Dim omega As Double
Dim OmegaL As Double, OmegaU
As Double
Dim w0 As Double
Dim BW As Double
Dim lp_s As Double
Dim theta
As Double
Dim sinh_val As Double
Dim cosh_val As Double
Dim alpha As Double,
beta As Double
Dim qmag2 As Double
Dim gamma_re As Double, gamma_im As Double
Dim delta_re As Double, delta_im As Double
Dim sqrt_re As Double, sqrt_im As
Double
Dim mag As Double
Dim p1_re As Double, p1_im As Double
Dim p2_re
As Double, p2_im As Double
Dim phase_sum As Double
Dim angle_k As Double
Dim x1 As Double, y1 As Double
Dim tmp As Double
Dim k As Integer
If
fL <= 0 Or fU <= fL Or N <= 0 Or r <= 0 Then
ChebyBSPhase = 0
Exit Function
End If
On Error GoTo ErrorHandler
' Convert Hz to
rad/s
OmegaL = TWOPI * fL
OmegaU = TWOPI * fU
omega = TWOPI * f
epsilon = Sqr(10 ^ (r / 10) - 1)
w0 = Sqr(OmegaL * OmegaU)
BW = OmegaU - OmegaL
' lp_s = asinh(1/epsilon) / N
tmp = 1# / epsilon
lp_s = Log(tmp + Sqr(tmp
* tmp + 1#)) / N
' sinh(lp_s), cosh(lp_s)
tmp = Exp(lp_s)
sinh_val
= 0.5 * (tmp - 1# / tmp)
cosh_val = 0.5 * (tmp + 1# / tmp)
phase_sum =
0#
For k = 1 To N
theta = PI * (2# * k - 1#) / (2# * N)
alpha = -sinh_val
* Sin(theta)
beta = cosh_val * Cos(theta)
qmag2 = alpha * alpha + beta
* beta
gamma_re = BW * alpha / qmag2
gamma_im = BW * (-beta) / qmag2
delta_re = gamma_re * gamma_re - gamma_im * gamma_im - 4# * w0 * w0
delta_im
= 2# * gamma_re * gamma_im
' Complex sqrt of delta (principal)
mag = Sqr(delta_re
* delta_re + delta_im * delta_im)
If mag = 0# Then
sqrt_re = 0#
sqrt_im
= 0#
Else
sqrt_re = Sqr((mag + delta_re) / 2#)
If delta_im > 0# Then
sqrt_im = Sqr((mag - delta_re) / 2#)
ElseIf delta_im < 0# Then
sqrt_im
= -Sqr((mag - delta_re) / 2#)
Else
sqrt_im = 0#
End If
End If
p1_re = (gamma_re + sqrt_re) / 2#
p1_im = (gamma_im + sqrt_im) / 2#
p2_re
= (gamma_re - sqrt_re) / 2#
p2_im = (gamma_im - sqrt_im) / 2#
' Ensure
LHP
If p1_re >= 0# Or p2_re >= 0# Then
sqrt_re = -sqrt_re
sqrt_im
= -sqrt_im
p1_re = (gamma_re + sqrt_re) / 2#
p1_im = (gamma_im + sqrt_im)
/ 2#
p2_re = (gamma_re - sqrt_re) / 2#
p2_im = (gamma_im - sqrt_im) / 2#
End If
' angle_k = Atan2(Omega - p_im, -p_re) (inline atan2)
' ---- pole
p1 ----
y1 = omega - p1_im
x1 = -p1_re
If x1 > 0# Then
angle_k =
Atn(y1 / x1)
ElseIf x1 < 0# Then
If y1 >= 0# Then
angle_k = Atn(y1
/ x1) + PI
Else
angle_k = Atn(y1 / x1) - PI
End If
Else
If y1 >
0# Then
angle_k = PI / 2#
ElseIf y1 < 0# Then
angle_k = -PI / 2#
Else
angle_k = 0#
End If
End If
phase_sum = phase_sum + angle_k
' ---- pole p2 ----
y1 = omega - p2_im
x1 = -p2_re
If x1 > 0# Then
angle_k = Atn(y1 / x1)
ElseIf x1 < 0# Then
If y1 >= 0# Then
angle_k
= Atn(y1 / x1) + PI
Else
angle_k = Atn(y1 / x1) - PI
End If
Else
If y1 > 0# Then
angle_k = PI / 2#
ElseIf y1 < 0# Then
angle_k = -PI
/ 2#
Else
angle_k = 0#
End If
End If
phase_sum = phase_sum + angle_k
Next k
ChebyBSPhase = -phase_sum * 180# / PI
' Wrap to [-180, 180]
Do While ChebyBSPhase > 180#
ChebyBSPhase = ChebyBSPhase - 360#
Loop
Do While ChebyBSPhase < -180#
ChebyBSPhase = ChebyBSPhase + 360#
Loop
Exit Function
|








