NEETS Module 9 - Introduction to Wave- Generation and Wave-Shaping
Pages i,
1-1,
1-11,
1-21,
1-31,
1-41,
2-1,
2-11,
2-21,
2-31,
3-1,
3-11,
3-21,
3-31,
3-41,
3-51,
4-1,
4-11,
4-21,
4-31,
4-41,
4-51, Index
| - |
Matter, Energy,
and Direct Current |
| - |
Alternating Current and Transformers |
| - |
Circuit Protection, Control, and Measurement |
| - |
Electrical Conductors, Wiring Techniques,
and Schematic Reading |
| - |
Generators and Motors |
| - |
Electronic Emission, Tubes, and Power Supplies |
| - |
Solid-State Devices and Power Supplies |
| - |
Amplifiers |
| - |
Wave-Generation and Wave-Shaping Circuits |
| - |
Wave Propagation, Transmission Lines, and
Antennas |
| - |
Microwave Principles |
| - |
Modulation Principles |
| - |
Introduction to Number Systems and Logic Circuits |
| - |
- Introduction to Microelectronics |
| - |
Principles of Synchros, Servos, and Gyros |
| - |
Introduction to Test Equipment |
| - |
Radio-Frequency Communications Principles |
| - |
Radar Principles |
| - |
The Technician's Handbook, Master Glossary |
| - |
Test Methods and Practices |
| - |
Introduction to Digital Computers |
| - |
Magnetic Recording |
| - |
Introduction to Fiber Optics |
| Note: Navy Electricity and Electronics Training
Series (NEETS) content is U.S. Navy property in the public domain. |
Chapter 1 - Tuned
CIRCUITS
Learning Objectives
Learning objectives are stated at the beginning of each chapter. These learning
objectives serve as a preview of the information you are expected to learn in the
chapter. The comprehensive check questions are based on the objectives. By successfully
completing the OCC/ECC, you indicate that you have met the objectives and have learned
the information. The learning objectives are listed below.
Upon completion of this chapter, you will be able to:
1. State the applications of a resonant circuit.
2. Identify the conditions that exist in a resonant circuit.
3. State and apply the formula for resonant frequency of an AC circuit.
4. State the effect of changes in inductance (L) and capacitance
(C) on resonant frequency (fr).
5. Identify the characteristics peculiar to a series resonant circuit.
6. Identify the characteristics peculiar to a parallel resonant circuit.
7. State and apply the formula for Q.
8. State what is meant by the bandwidth of a resonant circuit and
compute the bandwidth for a given circuit.
9. Identify the four general types of filters.
10. Identify how the series- and parallel-resonant circuit can be used as a bandpass or a band-reject filter.
Introduction to Tuned Circuits
When your radio or television set is turned on, many events take place within
the "receiver" before you hear the sound or see the picture being sent by the transmitting
station.

Figure 1-1A - Basic tuned circuits. SERIES Tuned Circuit.
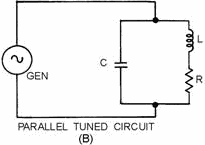
Figure 1-1B - Basic tuned circuits. PARALLEL Tuned Circuit.
Many different signals reach the antenna of a radio receiver at the same time.
To select a station, the listener adjusts the tuning dial on the radio receiver
until the desired station is heard. Within the radio or TV receiver, the actual
"selecting" of the desired signal and the rejecting of the unwanted signals are
accomplished by what is called a Tuned Circuit. a tuned circuit consists of a coil
and a capacitor connected in series or parallel. Later in this chapter you will
see the application and advantages of both series- and parallel-tuned circuits.
Whenever the characteristics of inductance and capacitance are found in a tuned
circuit, the phenomenon as RESONANCE takes place.
You learned earlier in the Navy Electricity and Electronics Training Series,
Module 2, chapter 4, that inductive reactance (XL) and capacitive reactance (XC)
have opposite effects on circuit impedance (Z).
You also learned that if the frequency applied to an LCR circuit causes XL
and XC to be equal, the circuit is RESONANT.
If you realize that XL and XC can be equal ONLY at
ONE Frequency (the resonant frequency), then you will have learned the most important
single fact about resonant circuits. This fact is the principle that enables tuned
circuits in the radio receiver to select one particular frequency and reject all
others. This is the reason why so much emphasis is placed on XL and XC
in the discussions that follow.
Examine figure 1-1. Notice that a basic tuned circuit consists of a coil and
a capacitor, connected either in series, view (A), or in parallel, view (B). The
resistance (R) in the circuit is usually limited to the inherent resistance of the
components (particularly the resistance of the coil). For our purposes we are going
to disregard this small resistance in future diagrams and explanations.
You have already learned how a coil and a capacitor in an AC circuit perform.
This action will be the basis of the following discussion about tuned circuits.
Why should you study tuned circuits? Because the tuned circuit that has been
described above is used in just about every electronic device, from remote-controlled
model airplanes to the most sophisticated space satellite.
You can assume, if you are going to be involved in electricity or electronics,
that you will need to have a good working knowledge of tuned circuits and how they
are used in electronic and electrical circuits.
REVIEW of Series/PARALLEL AC Circuits
First we will review the effects of frequency on a circuit which contains resistance,
inductance, and capacitance. This review recaps what you previously learned in the
Inductive and Capacitive Reactance chapter in module 2 of the NEETS.
Frequency EFFECTS ON RLC Circuits
Perhaps the most often used control of a radio or television set is the station
or channel selector. Of course, the volume, tone, and picture quality controls are
adjusted to suit the individual's taste, but very often they are not adjusted when
the station is changed. What goes on behind this station selecting? In this chapter,
you will learn the basic principles that account for the ability of circuits to
"tune" to the desired station.
Effect of Frequency on Inductive Reactance
In an AC circuit, an inductor produces inductive reactance which causes the current
to lag the voltage by 90 degrees. Because the inductor "reacts" to a changing current,
it is known as a reactive component. The opposition that an inductor presents to
AC is called inductive reactance (XL). This opposition is caused by the
inductor "reacting" to the changing current of the AC source. Both the inductance
and the frequency determine the magnitude of this reactance. This relationship is
stated by the formula:
XL = 2πfL
Where:
XL = the inductive reactance in ohms
f = the frequency in hertz
L = the inductance in henries
π
= 3.1416

Figure 1-2 - Effect of frequency on inductive reactance.
As shown in the equation, any increase in frequency, or "f," will cause a corresponding
increase of inductive reactance, or "XL." Therefore, the INDUCTIVE REACTANCE
VARIES DIRECTLY WITH the FREQUENCY. As you can see, the higher the frequency, the
greater the inductive reactance; the lower the frequency, the less the inductive
reactance for a given inductor. This relationship is illustrated in figure 1-2.
Increasing values of XL are plotted in terms of increasing frequency.
Starting at the lower left corner with zero frequency, the inductive reactance is
zero. As the frequency is increased (reading to the right), the inductive reactance
is shown to increase in direct proportion.
Effect of Frequency on Capacitive Reactance
In an AC circuit, a capacitor produces a reactance which causes the current to
lead the voltage by 90 degrees. Because the capacitor "reacts" to a changing voltage,
it is known as a reactive component. The opposition a capacitor presents to AC is
called capacitive reactance (XC). The opposition is caused by the capacitor
"reacting" to the changing voltage of the AC source. The formula for capacitive
reactance is:
XC = 1 / 2πfC
Where:
XC = the capacitive reactance in ohms
f = the frequency in hertz
C = the capacitance in farads
π = 3.1416
In contrast to the inductive reactance, this equation indicates that the CAPACITIVE
REACTANCE VARIES INVERSELY WITH The Frequency. When f = 0, XC is
infinite (∞) and decreases as frequency increases. That is, the lower the frequency,
the greater the capacitive reactance; the higher the frequency, the less the reactance
for a given capacitor.

Figure 1-3 - Effect of frequency on capacitive reactance.
As shown in figure 1-3, the effect of capacitance is opposite to that of inductance.
Remember, capacitance causes the current to lead the voltage by 90 degrees, while
inductance causes the current to lag the voltage by 90 degrees.
Effect of Frequency on Resistance
In the expression for inductive reactance, XL = 2πfL,
and in the expression for capacitive reactance,
XC = 1 / 2πfC
both contain "f" (frequency). Any change of frequency changes the reactance of
the circuit components as already explained. So far, nothing has been said about
the effect of frequency on resistance. In an Ohm's law relationship, such as R =
E/I no "f" is involved. Thus, for all practical purposes, a change of frequency
does not affect the resistance of the circuit. If a 60-hertz AC voltage causes 20
milliamperes of current in a resistive circuit, then the same voltage at 2000 hertz,
for example, would still cause 20 milliamperes to flow.
Note: Remember that the total opposition to AC is called impedance (Z). Impedance
is the combination of inductive reactance (XL), capacitive reactance
(XC), and resistance (R). When dealing with AC circuits, the impedance
is the factor with which you will ultimately be concerned. But, as you have just
been shown, the resistance (R) is not affected by frequency. Therefore, the remainder
of the discussion of AC circuits will only be concerned with the reactance of inductors
and capacitors and will ignore resistance.
AC Circuits Containing Both Inductive and Capacitive Reactances
AC circuits that contain both an inductor and a capacitor have interesting characteristics
because of the opposing effects of L and C. XL and XC
may be treated as reactors which are 180 degrees out of phase. As shown in figure
1-2, the vector for XL should be plotted above the baseline; vector for
XC, figure 1-3, should be plotted below the baseline. In a series circuit,
the effective reactance, or what is termed the RESULTANT REACTANCE, is the difference
between the individual reactances. As an equation, the resultant reactance is:
X = XL - XC
Suppose an AC circuit contains an XL of 300 ohms and an XC of 250 ohms.
The resultant reactance
X = XL - XC = 300 - 250 =
50 ohms (inductive)
In some cases, the XC may be larger than the XL.
If XL = 1200 ohms and XC = 4000 ohms, the difference
is: X = XL - XC = 1200 - 4000 = -2800 ohms (capacitive).
The total carries the sign (+ or -) of the greater number (factor).
Q-1. What is the relationship between frequency and the values of
(a) XL, (b) XC, and (c) R?
Q-2. In an AC circuit that contains both an inductor and a capacitor,
what term is used for the difference between the individual reactances?
RESONANCE
For every combination of L and C, there is only ONE frequency (in both series
and parallel circuits) that causes XL to exactly equal XC;
this frequency is known as the RESONANT Frequency. When the resonant frequency is
fed to a series or parallel circuit, XL becomes equal to XC,
and the circuit is said to be RESONANT to that frequency. The circuit is now called
a RESONANT Circuit; resonant circuits are tuned circuits. The circuit condition
wherein XL becomes equal to XC is known as
RESONANCE
Each LCR circuit responds to resonant frequency differently than it does to any
other frequency. Because of this, an LCR circuit has the ability to separate frequencies.
For example, suppose the TV or radio station you want to see or hear is broadcasting
at the resonant frequency. The LC "tuner" in your set can divide the frequencies,
picking out the resonant frequency and rejecting the other frequencies. Thus, the
tuner selects the station you want and rejects all other stations. If you decide
to select another station, you can change the frequency by tuning the resonant circuit
to the desired frequency.
RESONANT Frequency
As stated before, the frequency at which XL equals XC
(in a given circuit) is known as the resonant frequency of that circuit. Based on
this, the following formula has been derived to find the exact resonant frequency
when the values of circuit components are known:
fr = 1 / [2π √(LC)]
There are two important points to remember about this formula. First, the resonant
frequency found when using the formula will cause the reactances (XL
and XC) of the L and C components to be equal. Second, any change in
the value of either L or C will cause a change in the resonant frequency.
An increase in the value of either L or C, or both L and C, will lower the resonant
frequency of a given circuit. a decrease in the value of L or C, or both L and C,
will raise the resonant frequency of a given circuit.
The symbol for resonant frequency used in this text is f. Different texts and
references may use other symbols for resonant frequency, such as fo,
Fr, and fR. The symbols for many circuit parameters have
been standardized while others have been left to the discretion of the writer.
When you study, apply the rules given by the writer of the text or reference; by
doing so, you should have no trouble with
nonstandard symbols and designations.
The resonant frequency formula in this text is:
fr = 1 / [2π √(LC)]
Where:
fr = the resonant frequency in Hertz
L = the inductance in Heries
C = the capacitance in Farads
π = 3.1416
By substituting the constant .159 for the quantity
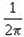
the formula can be simplified to the following:

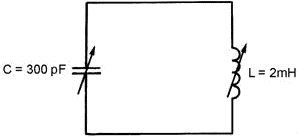
Figure 1-4 - Practice tank circuit.
Let's use this formula to figure the resonant frequency (fr). The
circuit is shown in the practice tank circuit of figure 1-4.
Given:
L = 2 mH (2 x 10-3 H)
C = 300 pF (300 x 10-12 F)
Solution:

The important point here is not the formula nor the mathematics. In fact, you
may never have to compute a resonant frequency. The important point is for you to
see that any given combination of L and C can be resonant at only one frequency;
in this case, 205 kHz.
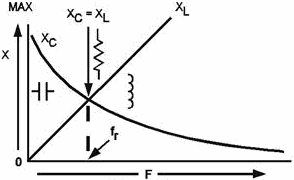
Figure 1-5 - Relationship between XL and XC
as frequency increases.
The universal reactance curves of figures 1-2 and 1-3 are joined in figure 1-5
to show the relative values of XL and XL at resonance, below
resonance, and above resonance.
First, note that fr, (the resonant frequency) is that frequency (or
point) where the two curves cross. At this point, and ONLY this point, XL
equals XC. Therefore, the frequency indicated by fr
is the one and only frequency of resonance. Note the resistance symbol which indicates
that at resonance all reactance is cancelled and the circuit impedance is effectively
purely resistive. Remember, AC circuits that are resistive have no phase shift between
voltage and current. Therefore, at resonance, phase shift is cancelled. The phase
angle is effectively zero.
Second, look at the area of the curves to the left of fr. This area
shows the relative reactances of the circuit at frequencies BELOW resonance. To
these LOWER frequencies, XC will always be greater than XL.
There will always be some capacitive reactance left in the circuit after all inductive
reactance has been cancelled. Because the impedance has a reactive component, there
will be a phase shift. We can also state that below fr the circuit
will appear capacitive.
Lastly, look at the area of the curves to the right of f. This area shows the
relative reactances of the circuit at frequencies ABOVE resonance. To these HIGHER
frequencies, XL will always be greater than XC. There will
always be some inductive reactance left in the circuit after all capacitive reactance
has been cancelled. The inductor symbol shows that to these higher frequencies,
the circuit will always appear to have some inductance. Because of this, there will
be a phase shift.
RESONANT Circuits
Resonant circuits may be designed as series resonant or parallel resonant. Each
has the ability to discriminate between its resonant frequency and all other frequencies.
How this is accomplished by both series- and parallel-LC circuits is the subject
of the next section.
Note: Practical circuits are often more complex and difficult to understand than
simplified versions. Simplified versions contain all of the basic features of a
practical circuit, but leave out the nonessential features. For this reason, we
will first look at the IDEAL Series-RESONANT Circuit - a circuit that really doesn't
exist except for our purposes here.
The IDEAL SERIES-RESONANT Circuit
The ideal series-resonant circuit contains no resistance; it consists of only
inductance and capacitance in series with each other and with the source voltage.
In this respect, it has the same characteristics of the series circuits you have
studied previously. Remember that current is the same in all parts of a series circuit
because there is only one path for current.
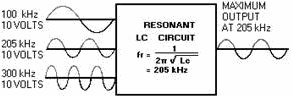
Figure 1-6. - Output of the resonant circuit.
Each LC circuit responds differently to different input frequencies. In the following
paragraphs, we will analyze what happens internally in a series-LC circuit when
frequencies at resonance, below resonance, and above resonance are applied. The
L and C values in the circuit are those used in the problem just studied under resonant-frequency.
The frequencies applied are the three inputs from figure
1-6. Note that the resonant frequency of each of these components is 205 kHz,
as figured in the problem.
How the Ideal Series-LC Circuit Responds to the Resonant Frequency (205 kHz)
Given:

Note: You are given the values of XL, XC, and fr
but you can apply the formulas to figure them. The values given are rounded off
to make it easier to analyze the circuit.
First, note that XL and XC are equal. This shows that the
circuit is resonant to the applied frequency of 205 kHz. XL and XC
are opposite in effect; therefore, they subtract to zero. (2580 ohms - 2580 ohms
= zero.) At resonance, then, X = zero. In our theoretically perfect circuit with
zero resistance and zero reactance, the total opposition to current (Z) must also
be zero.
|

















