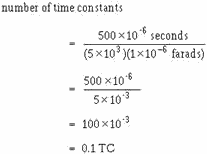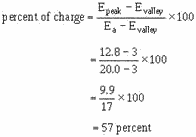Navy Electricity and Electronics Training Series (NEETS)
Module 9 - Introduction to Wave- Generation and Wave-Shaping
Chapter 3:  Pages 3-31 through 3-40

PRT is too short, some of the triggers occur when the base is far below cutoff. The blocking oscillator may then synchronize with every second or third sync pulse.
 
For example, in figure 3-37, view (A) and view (B) if trigger pulses are applied every 200 microseconds (5 kilohertz), the trigger that appears at T1 is not of sufficient amplitude to overcome the cutoff bias and turn on Q1. At T2, capacitor C1 has nearly discharged and the trigger causes Q1 to conduct. Note that with a 200-microsecond input trigger, the output PRT is 400 microseconds. The output frequency is one-half the input trigger frequency and the blocking oscillator becomes a frequency divider.
 
Q10.   What component in a blocking oscillator controls pulse width?
 
TIME-BASE GENERATORS
 
Radar sets, oscilloscopes, and computer circuits all use sawtooth (voltage or current) waveforms. A sawtooth waveshape must have a linear rise. The sawtooth waveform is often used to produce a uniform, progressive movement of an electron beam across the face of an electrostatic cathode ray tube. This movement of the electron beam is known as a SWEEP. The voltage which causes this movement is known as SWEEP VOLTAGE and the circuit which produces this voltage is the SWEEP GENERATOR, or TIME-BASE GENERATOR. Most common types of time-base generators develop the sawtooth waveform by using some type of switching action with either the charge or discharge of an RC or RL circuit.
 
Sawtooth Wave
 
A sawtooth wave can be generated by using an RC network. Possibly the simplest sawtooth generator is that which is shown in figure 3-38, view (A). Assume that at T0 (view (B)), S1 is placed in position P. At the instant the switch closes, the applied voltage (E_a) appears at R. C begins to charge to E_a through R. If S1 remains closed long enough, C will fully charge to E_a. You should remember from NEETS, Module 2, Alternating Current and Transformers, that a capacitor takes 5 time constants (5TC) to fully charge. As the capacitor charges to the applied voltage, the rate of charge follows an exponential curve. If a linear voltage is desired, the full charge time of the capacitor cannot be used because the exponential curve becomes nonlinear during the first time constant.
 

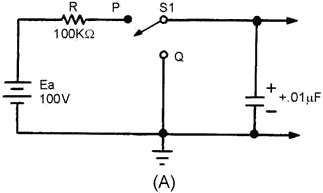
Figure 3-38A. - Series RC circuit.

3-31

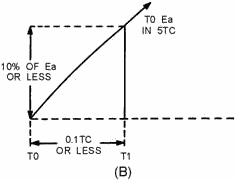
Figure 3-38B. - Series RC circuit.

However, during the first 10 percent of the first time constant, the rate of voltage change across the capacitor is almost constant (linear). Suppose that S1 is placed in position P at T0, and C is allowed to charge for 0.1 time constant. This is shown as T0 to T1 in view (B). Notice that the rate of voltage change across C is nearly constant between T0 and T1. Now, assume that at T1 the switch is moved from position P to position Q. This shorts the capacitor, and it discharges very rapidly. If the switch is placed back in position P, the capacitor will start charging again.
 
By selecting the sizes of R and C, you can have a time constant of any value you desire. Further, by controlling the time S1 remains closed, you can generate a sawtooth of any duration. Figure 3-39 is the Universal Time Constant Chart. Notice in the chart that if 1 time constant is 1,000 microseconds, S1 (figure 3-38, view (A )) can be closed no longer than 100 microseconds to obtain a reasonable linear sawtooth. In this example, C1 will charge to nearly 10 volts in 0.1 time constant.

3-32

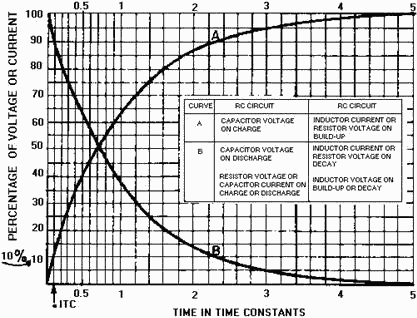
Figure 3-39. - Universal Time Constant Chart.

The dimensions of the sawtooth waveform used in oscilloscopes need to be discussed before going any further. Figure 3-40 shows a sawtooth waveform with the various dimensions labeled. The duration of the rise of voltage (T0 to T1) is known as the SWEEP TIME or ELECTRICAL LENGTH. The electron beam of an oscilloscope moves across the face of the cathode ray tube during this sweep time. The amount of voltage rise per unit of time is referred to as the SLOPE of the waveform. The time from T1 to T2 is the capacitor discharge time and is known as FALL TIME or FLYBACK TIME. This discharge time is known as flyback time because during this period the electron beam returns, or "flys" back, from the end of a scanning line to begin the next line.

3-33

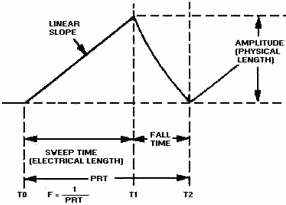
Figure 3-40. - Sawtooth waveform.

The amplitude of the rise of voltage is known as the PHYSICAL LENGTH. It is called physical length because the greater the peak voltage, the greater physical distance the beam will move. For example, the amount of voltage needed to move an electron beam 4 inches is twice the amount needed to move the beam 2 inches across the face of a given CRT

The voltage rise between T0 to T1 is the LINEAR SLOPE of the wave. The linearity of the rise of voltage is determined by the amount of time the capacitor is allowed to charge. If the charge time is kept short (10 percent or less of 1TC), the linearity is reasonably good.
 
As stated in the discussion of time-base generators, the waveform produced from any sawtooth generator must be linear. A LINEAR SAWTOOTH is one that has an equal change in voltage for an equal change in time. Referring to the Universal Time Constant Chart in figure 3-39, you can see that the most desirable part of the charge curve is the first one-tenth (0.1) of the first TC.
 
Figure 3-41, view (A), is a transistor sawtooth generator. In this figure R1 is a forward-biasing resistor for Q1, C1 is a coupling capacitor, and Q1 is serving as a switch for the RC network consisting of R2 and C2. With forward bias applied to Q1, the generator conducts at saturation, and its collector voltage (the output) is near 0 volts as indicated by the waveform in view (B). The charge felt by C1 is nearly 0. A negative gate is applied to the base of Q1 to cut off Q1 and allow C2 to charge. The length of time that the gate is negative determines how long Q1 will remain cut off and, in turn, how long C2 will be allowed to charge. The length of time that C2 is allowed to charge is referred to as the electrical length of the sawtooth that is produced.

3-34

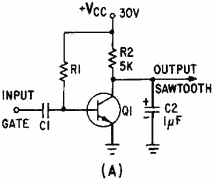
Figure 3-41A. - Transistor sawtooth generator.

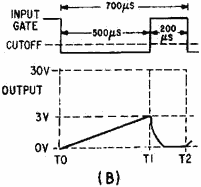
Figure 3-41B. - Transistor sawtooth generator.

The amplitude of the sawtooth that is produced is limited by the value of V_CC  that is used in the circuit. For example, if the voltage is 30 volts, and the capacitor (C2) is allowed to charge to 10 percent of 30 volts, then the amplitude of the sawtooth will be 3 volts (see figure 3-41, view (B)). If VCC  is increased to 40 volts, C2 will charge to 10 percent of 40 volts and the output will increase in amplitude to 4 volts. Changing the value of V_CC  in the circuit changes the amplitude of the sawtooth waveform that is produced; amplitude determines the physical length. Since the number of time constants used in the circuit has not been changed, linearity does not change with a change in V_CC.
 
The linear slope that is produced by the circuit is dependent on two variables; (1) the time constant of the RC circuit and (2) the gate length of the gate applied to the circuit. The circuit will produce a linear sawtooth waveshape if the components selected are such that only one-tenth of 1 TC or less is used. The GATE LENGTH is the amount of time that the gate is applied to the circuit and controls the time that the capacitor is allowed to charge. The value of R2 and C2 determines the time for 1 time constant

3-35

(TC = RC). To determine the number of time constants (or the fraction of 1TC) used, divide the time for 1 time constant into the time that the capacitor is allowed to charge:

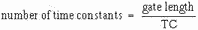
In figure 3-41, view (B), gate length is 500 microseconds and TC is the product of R2 (5 kilohms) and C2 (1 microfarad). The number of time constants is computed as follows:

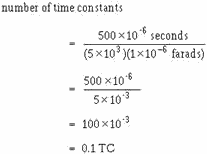
Therefore, 0.1TC is the length of time required to produce a linear rise in the sawtooth waveform.

shows that an increase in gate length increases the number of time constants. An increase in the number of time constants decreases linearity. The reason is that C2 now charges to a greater percentage of the applied voltage, and a portion of the charge curve is being used that is less linear. The waveform in figure 3-42, view (A), shows an increase in amplitude (physical length), an increase in the time that C2 is allowed to charge (electrical length), and a decrease in linearity. If a smaller percentage of V_CC  is used, the gate length is decreased. As shown in view (B), this decreased gate length results in an increase in linearity, a decrease in the time that C2 is allowed to charge (electrical length), and a decrease in amplitude (physical length).

3-36

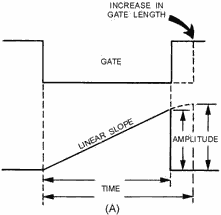
Figure 3-42A. - Relationship of gate to linearity.

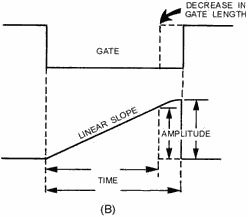
Figure 3-42B. - Relationship of gate to linearity.

Changing the value of R and C in the circuit affects linearity since they control the time for 1 time constant. For example, if the value of C2 is increased in the circuit, as shown in figure 3-43, view (A), the time for 1 time constant increases and the number of time constants then decreases. With a decrease in the number of time constants, linearity increases. The reason is that a smaller percentage of V_CC  is used, and the circuit is operating in a more linear portion of the charge curve. Increasing the value of the TC (C2 or R2) decreases the amplitude of the sawtooth (physical length) because C2 now charges to a smaller percentage V_CC  for a given time. The electrical length remains the same because the length of time that C2 is allowed to charge has not been changed.

3-37

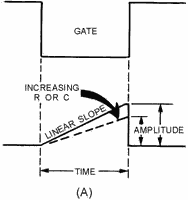
Figure 3-43A. - Relationship of R and C to linearity.

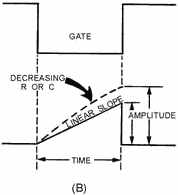
Figure 3-43B. - Relationship of R and C to linearity.

Decreasing the value of the TC (R2 or C2), as shown in figure 3-43, view (B), results in an increase in the number of time constants and therefore causes linearity to decrease. Anytime the number of time constants increases, the percentage of charge increases (see the Universal Time Constant Chart, figure 3- 39), and amplitude (physical length) increases. Without an increase in gate length, the time that C2 is allowed to charge through R2 remains the same; therefore, electrical length remains the same. Linearity is affected by gate length, the value of R, and the value of C; but is not affected by changing the value of VCC. Increasing the gate length decreases linearity, and decreasing gate length increases linearity. Increasing R or C in the circuit increases linearity, and decreasing R or C in the circuit decreases linearity.
 
The entire time of the sawtooth, from the time at which the capacitor begins charging (T0 in figure
3-41, view (B)) to the time when it starts charging again (T2), is known as the PRT of the wave. The pulse repetition frequency of the sawtooth wave is:

3-38

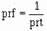
UNIJUNCTION SAWTOOTH GENERATOR. - So far, you have learned in this chapter that a switch and an RC network can generate a sawtooth waveform. When using a unijunction transistor as the switch, a simple sawtooth generator looks like the circuit in figure 3-44, view (A); the output waveshapes are shown in view (B). You may want to review unijunction transistors in NEETS, Module 7, Introduction to Solid-State Devices and Power Supplies, chapter 3, before continuing.

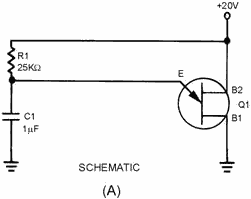
Figure 3-44A. - Unijunction sawtooth generator. SCHEMATIC.

When the 20 volts is applied across B2 and B1, the n-type bar acts as a voltage- divider. A voltage of 12.8 volts appears at a point near the emitter. At the first instant, C1 has no voltage across it, so the output of the circuit, which is taken across the capacitor (C1), is equal to 0 volts. (The voltage across C1 is also the voltage that is applied to the emitter of the unijunction.) The unijunction is now reverse biased. After T0, C1 begins to charge toward 20 volts.
 
At T1, the voltage across the capacitor (the voltage on the emitter) has reached approximately 12.8 volts. This is the peak point for the unijunction, and it now becomes forward biased. With the emitter forward biased, the impedance between the emitter and B1 is just a few ohms. This is similar to placing a short across the capacitor. The capacitor discharges very rapidly through the low resistance of B1 to E.
 
As C1 discharges, the voltage from the emitter to B1 also decreases. Q1 will continue to be forward biased as long as the voltage across C1 is larger than the valley point of the unijunction.
 
At T2 the 3-volt valley point of the unijunction has been reached. The emitter now becomes reverse biased and the impedance from the emitter to B1 returns to a high value. Immediately after T2, Q1 is reverse biased and the capacitor has a charge of approximately 3 volts. C1 now starts to charge toward 20 volts as it did originally (just after T0). This is shown from T2 to T3 in figure 3-44, view (B).

3-39

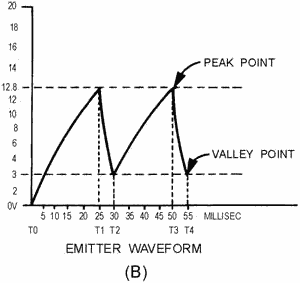
Figure 3-44B. - Unijunction sawtooth generator. EMITTER WAVEFORM.

The circuit operation from now on is just a continuous repetition of the actions between T2 and T4. The capacitor charges until the emitter becomes forward biased, the unijunction conducts and C1 discharges, and Q1 becomes reverse biased and C1 again starts charging.
 
Now, let's determine the linearity, electrical length, and amplitude of the output waveform. First, the linearity: To charge the circuit to the full 20 volts will take 5 time constants. In the circuit shown in figure 3-44, view (B), C1 is allowed to charge from T2 to T3. To find the percentage of charge, use the equation:

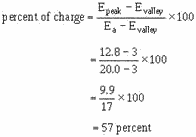
This works out to be about 57 percent and is far beyond the 10 percent required for a linear sweep voltage. The linearity is very poor in this example.

3-40

NEETS Table of Contents

• Introduction to Matter, Energy, and Direct Current
• Introduction to Alternating Current and Transformers
• Introduction to Circuit Protection, Control, and Measurement
• Introduction to Electrical Conductors, Wiring Techniques, and Schematic Reading
• Introduction to Generators and Motors
• Introduction to Electronic Emission, Tubes, and Power Supplies
• Introduction to Solid-State Devices and Power Supplies
• Introduction to Amplifiers
• Introduction to Wave-Generation and Wave-Shaping Circuits
• Introduction to Wave Propagation, Transmission Lines, and Antennas
• Microwave Principles
• Modulation Principles
• Introduction to Number Systems and Logic Circuits
• Introduction to Microelectronics
• Principles of Synchros, Servos, and Gyros
• Introduction to Test Equipment
• Radio-Frequency Communications Principles
• Radar Principles
• The Technician's Handbook, Master Glossary
• Test Methods and Practices
• Introduction to Digital Computers
• Magnetic Recording
• Introduction to Fiber Optics