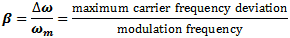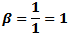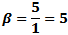Frequency Modulation

Frequency modulation uses the instantaneous amplitude of a modulating signal (voice, music, data, etc.) to directly vary the frequency of a carrier signal. Modulation index, β, is used to describe the ratio of maximum frequency deviation of the carrier to the maximum frequency deviation of the modulating signal. The concept was pioneered by Edwin H. Armstrong in the late 1920s and patented in the early 1930s.

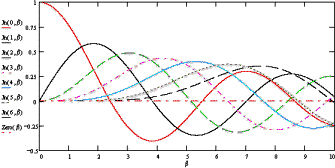
Depending on the modulation index chosen, the carrier and certain sideband frequencies may actually be suppressed. Zero crossings of the Bessel functions, J_n(β), occur where the corresponding sideband, n, disappears for a given modulation index, β. The composite spectrum for a single tone consists of lines at the carrier and upper and lower sidebands (of opposite phase), with amplitudes determined by the Bessel function values at those frequencies.

Modulation Index

Narrowband FM (NBFM)

Narrowband FM is defined as the condition where β is small enough to make all terms after the first two in the series expansion of the FM equation negligible.

Narrowband Approximation: β = Δω/Ω_m < 0.2 (could be as high as 0.5, though)

BW ~ 2ω_m

Wideband FM (WBFM)

Wideband FM is defined as when a significant number of sidebands have significant amplitudes.

BW ~ 2Δω

Carson's Rule

J.R. Carson showed in the 1920's that a good approximation that for both very small and very large β,

BW ~ 2 (Δω + Ω_m)) = 2*Ω_m (1 + β)

In the following examples, the carrier frequency is eleven time the modulation frequency. Red (dashed) lines represent the modulation envelope. Blue (solid) lines represent the modulated carrier.

Modulation Index (β) = 1

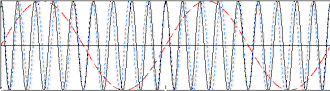
Here, the maximum frequency (f_max) causes a maximum deviation of 1*f_max in the carrier. From the modulation index formula:

Modulation Index (β) = 5

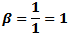
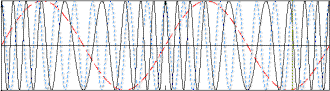
Here, the maximum frequency (f_max) causes a maximum deviation of 5*f_max in the carrier. From the modulation index formula:

Modulation Index (β) = 25

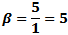
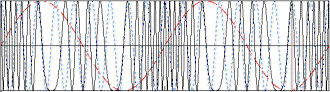
Here, the maximum frequency (f_max) causes a maximum deviation of 25*f_max in the carrier. From the modulation index formula:

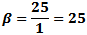
Note: FM waveforms created with MathCAD 4.0 software.