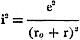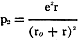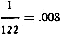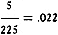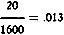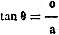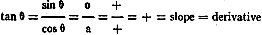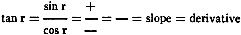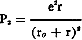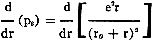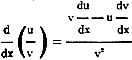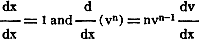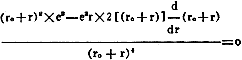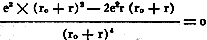|
March 1933 Radio News
 [Table
of Contents] [Table
of Contents]
Wax nostalgic about and learn from the history of early
electronics. See articles from
Radio & Television News, published 1919-1959. All copyrights hereby
acknowledged.
|
It has been a while since I saw
the quotient rule for derivatives applied. Probably the last time was in a college
text book, because I'm pretty sure I haven't had the occasion to use it since then
- except maybe back in the days when I was writing my
RF
Workbench software and needed to derive closed form solutions for group delay
in filters. This 1933 article from Radio News magazine presented the quotient
rule as part of a discussion for finding the impedance of a load for maximum power
transfer. Pure resistances were used in the example, but the method applies as well
to complex impedances. See also
National Radio
Institute advertisement, December 1954 Radio News;
Mathematics in Radio in July 1932 Radio News;
Measuring Inductance and Capacity, June 1931 Radio-Craft;
Mathematics in Radio,
March 1933 Radio News;
Radio Frequencies and Their Allocation, June | July 1940 National Radio News;
Your Radio Training and the Defense Program, December 1940 | January 1941
National Radio News.
Calculus and Its Application in Radio - Part Twenty
By J. E. Smith*
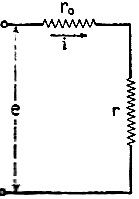
Figure 1 - Series resistor network.

Figure 2 - Power curve.
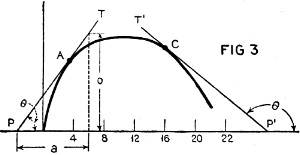
Figure 3 - Tangents to a curve.
In order to prove a very important and fundamental relation in the application
of calculus to radio circuits, let us investigate the simple series circuit of Figure
1. The current through this circuit is:
(1) 
The power delivered to the output resistance r is:
(2) p2 = i2 R
Now, from (1):
(3) 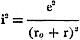
and substituting this value of i2 in (2) we have :
(4) 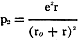
In the above equation, let e = 1 and r0 = 10 ohms. Tabulating the
results of p2 for various values of r, we have:
When r = 0, the corresponding value of p2 = 0
When r = 1, the corresponding value of p2 =
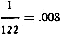
When r = 5, the corresponding value of p2 =
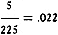
When r = 10, the corresponding value of p2 =

When r = 12, the corresponding value of p2 =

When r = 15, the corresponding value of p2 =

When r = 20, the corresponding value of p2 =
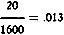
Plotting these values graphically as shown in Figure 2, we find that the maximum
power occurs when the output resistance r is equal to 10 ohms. But this was also
the value for the resistance r0, so it can be concluded that the maximum
power in an output resistance in a circuit similar to Figure 1 is obtained when
the output resistance is equal to the internal resistances of the other parts of
the circuit r0.
In this simple case it was rather easy to plot the values of the variables and
note the condition of maximum power. But there are many equations which are rather
involved and where this method would be rather inconvenient. Let us investigate
the possible use of calculus for solving this type of problem. It will be necessary
at this time to point out a few additional and simple theorems of the fundamental
calculus. Let us refer to the curve of Figure 3, which is similar to the one shown
in the previous figure. The direction of such a curve at any point can be defined
to be the same as the direction of the line tangent to the curve at that point.
Therefore, a line PT tangent to the curve at point A will have an angle expressed
as follows:
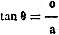
We have previously learned that this is represented as the slope and is the value
of the derivative at that point. It will be noticed that as the function is increasing,
this tangent line will in general be making an acute angle with the axis of x. It
will be equal to a positive number, since the sin θ = 0, and cos θ =
a are in the first quadrant and have positive values:
thus:
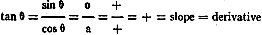
When the function is decreasing, a tangent line drawn at any point such as C
in Figure 3 will be making an obtuse angle "θ" with the axis of x. It will
therefore be equal to a negative number; thus:
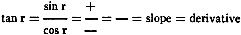
From the above analysis, since the derivative is a positive number up to the
maximum point of the curve and a negative number beyond this point, it follows that
at the maximum point it must be equal to zero.
This very important relation gives us a method of solving the following equation
for the appropriate value of r.
(a) 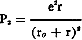
In order that the power p2 become a maximum, it follows:
(b) 
Solving:
(c) 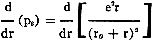
The solution of equation c appears to be a little complicated, but it is simply
an application of the elementary forms of differentiation. Showing the intermediate
steps of the solution, we have, first, the derivative of a quotient which is of
the form:
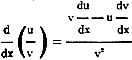
Solving:(d) 
Second, it will be recalled:
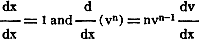
Then (d) becomes:
(e) 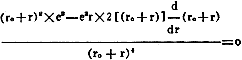
This becomes:
(f) 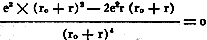
* President, National Radio Institute.
Posted December 3, 2021
(updated from original post on 3/25/2014)
|