|
The following equations and images describe electromagnetic waves inside both rectangular waveguide and circular
(round) waveguides. Oval waveguide equations are not included due to the mathematical complexity.
Click here for a transmission
lines & waveguide presentation.
A Cavity Resonance Calculator is included in
Espresso Engineering Workbook™ for FREE.
Rectangular Waveguide Cutoff Frequency
|
The lower cutoff frequency (or wavelength) for a particular mode in rectangular
waveguide is determined by the following equations (note that the length, x, has no bearing
on the cutoff frequency):
|
This example is for TE1,0 (the mode with the lowest cutoff frequency)
in WR284 waveguide (commonly used for S-band radar systems). It has a width of
2.840" (7.214 cm) and a height of
1.340"(3.404 cm).
Espresso Engineering Workbook™
|
| where |
a = b = m = n = ε
= µ = |
Inside width (m), longest dimension Inside height (m), shortest dimension Number of ½-wavelength
variations of fields in the "a" direction Number of ½-wavelength variations of fields in the "b" direction
Permittivity (8.854187817E-12 for free space) Permeability
(4πE-7 for
free space) |
|
|
The TE10 mode is the dominant mode of a rectangular waveguide with a>b, since it has the lowest
attenuation of all modes. Either m or n can be zero, but not both.
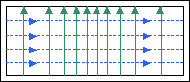
End View (TE10)
Side View (TE10)
Top View (TE10)
____ Electric field lines p
_ _ _ Magnetic field lines
|
For TM modes, m=0 and n=0 are not possible, thus, TM11 is the lowest possible TM mode.
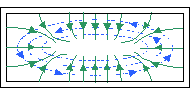
End View (TM11)
Side View (TM11)
____ Electric field lines
_ _ _ Magnetic field lines
|
|
|
The lower cutoff frequency (or wavelength) for a particular TE mode in circular waveguide is determined by
the following equation:
 ,
where p'mn is
| 0 |
3.832 |
7.016 |
10.174 |
| 1 |
1.841 |
5.331 |
8.536 |
| 2 |
3.054 |
6.706 |
9.970 |
|
|
The lower cutoff frequency (or wavelength) for a particular TM mode in circular waveguide is determined by
the following equation:
(m), where pmn is
| 0 |
2.405 |
5.520 |
8.654 |
| 1 |
3.832 |
7.016 |
10.174 |
| 2 |
5.135 |
8.417 |
11.620 |
|
Related Pages on RF Cafe
|
