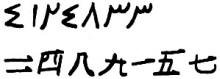[Index] [Index]
Reproduced here are various Mathematical Puzzles from
The Old Farmer's Almanac,
published continuously since 1792. All copyrights hereby acknowledged.
|
Here is a nice collection of
mathematical puzzles from the 1988 edition of the Old Farmer's Almanac.
As always, they range in difficulty from Level 1 (easiest) to Level 5 (most
difficult). Solutions are provided for all but Level 5. Readers were invited to
submit their solutions, and then winners were announced in the next year's
edition. If you wanted to see the results, you needed to write and request them
(and pay mailing cost). The first couple puzzles are very familiar. Puzzle 5
requires either some simple algebra for multiple equations in multiple unknowns,
or you can get it with trial and error while zeroing in on the answer. By the
time you get to Puzzle 9, you'll need to be a serious Puzzler to spend time on
it. In 1988, there were not easily accessed calculators and solvers for just
about every need. Puzzle 11 wants you to find the prime factors of
2,095,632,000. I easily found them in about 30 seconds, including the time
needed to do a search for this
Prime Factorization Calculator. If you solve Puzzle 13, you're definitely a
geometer akin to
Euclid and Pythagoras.
Old and New Mathematical Puzzles
Blanton C. Wiggin, Puzzle Editor
Here are 15 puzzles for 1988 from our readers, with something to interest everyone.
They are challenging, but everyday common sense and a little agility are all you'll
need; you won't need calculus, computers, alertness to tricks, or specialized knowledge,
although these are sometimes helpful. For some puzzles you may require a chart or
data from your local library or a dictionary.
We will award one prize of $50 for the best set of solutions to puzzles 12 through
15 received before February 1, 1988. The answers to these four are omitted here.
We use a point system to judge the prize set. A basic, unadorned, correct answer
is 20 points. For a thorough analysis, an elegant or novel answer, up to 5 points
extra. Numerical errors lose only 2 or 3 points, if it is clear that the method
is understood.
Explanations and Prize-Set Answers will be sent after June 15 to anyone sending
50¢ and a self-addressed stamped envelope to "Puzzle Answers," The Old Farmer's
Almanac, Dublin, New Hampshire 03444.
We will also pay $15 for any original puzzles we use in The Old Farmer's Almanac
for 1989. Closing date for submissions is February 1, 1988. Entries become the property
of Yankee Publishing Incorporated and cannot be acknowledged or returned. In addition
to submitting a puzzle, please tell us the type of puzzle you like best, such as
magic squares, geometry, time-rate-quantity, mazes, logic, number substitutions,
etc.
Frequent entrant Bob Symons, Waterloo, Ontario, is the 1987 winner, followed
by Paul Nektaredes, Tarpon Springs, Florida. Congratulations, all!
Have fun with these 1988 puzzles, and send your answers early for puzzles 12-15.
Please use a separate sheet for each puzzle or answer. Be sure to put your name
and address on each sheet. Good luck!
Answers appear on page 218.
1. Penny Piles
Difficulty: 1
Can you arrange seven pennies in five straight rows with three pennies in each
row? The rows can go in any direction. Scott Jenks
Hortonville, Wisconsin
2. Double Your Money
Difficulty: 1
If you've doubled your money since the OFA last published this classic in 1976,
you've done well. Little Roger however, plans to do better. At the beginning of
January 1988, he plans to be more thrifty: on the first day of the month to save
1 penny; on the second day of the month to save double the amount - 2 pennies. On
the third he wants to again save twice the previous day's or 4 cents, and so on,
for a month.
How much will Roger have on the 31st of January, each day doubling the amount
of money saved the day before Marion Dykstra
Knoxville, Iowa
 3. Cross Only Once 3. Cross Only Once
Difficulty: 2
Using one continuous line, try to cross each of the 16 line segments only once.
Do not miss one or cross any line twice.
Mildred Summers
Jersey Ville, Illinois
4. Assorted Animals
Difficulty: 2
One hundred years ago, Farmer Jones bought 100 animals for $100.
What was the mix of cows at $10, sheep at $2.50, and pigs at 50¢ each?
Albert Jackson
Morrill, Maine
5. The Great Migration
Difficulty: 2
Three fowl race 3,000 miles south to their wintering grounds.
A mallard leaves on Almanac publication day and flies at 25 mph for 10 hours
per day with three days of rest stops along the way.
A Canada goose leaves the next day, and flies at 30 mph for 10 hours per day
with just one day for a rest stop.
A common loon leaves 3 days after the mallard and flies at 40 mph for 10 hours
per day with two days of rest along the way.
Which bird will arrive first?
Gary R. Shawley
Warren, Pennsylvania
6. Quick Ranking
Difficulty: 2
Ann, Betty, Carol, and Dotty won't tell outsiders their ages, but will answer
Yes-No questions such as: "Dotty, are you older than Betty?" How few questions will
always disclose the order of their ages?
Jerry Curtright
Carpentersville, Illinois
7. Calendar Trivia
Difficulty: 3
a) In the 1960s or 1970s, someone told me he had just played a golf course that
had been open to the public that day, a Saturday. He explained that the course was
open to the public only on the third Saturday and third Sunday of each month. I
had wanted to play there, so the next day I went. To my disappointment, I found
the links closed. The next month the same thing happened. On a Saturday evening
I was reminded that the golf course had been open that day to the public. So off
I went again the next day, and again I found it closed.
In what year did this happen?
Robert Assaly
Cambridge, Massachusetts
b) Al, Bill, Cal, and Doug were all born on May 12, but in 1964, 1965, 1966,
and 1967 respectively. Who will be the oldest on his 21st birthday?
c) An old man will celebrate his birthday on February 29, 1988. It will be the
5th time during his life that his birthday falls on Monday. Here "birthday" includes
the day he was born.
How old will he be?
John Brendel
Astoria, New York
8. Overcounting
Difficulty: 3
a) Several tribes of ancients counted in a different manner than we do.
They would say "1 in the 7th decade," for our 61. Or "3, 5th decade, 9th hundred,"
for our 843, today. This has been called "overcounting," a perfectly logical and
consistent system, with vestigial words surviving in a few places today.
Assuming they used our symbols, place value, and the zero, here are some ancient
overcounting quantities:
2727
511
31289
How would we express them?
b) Arabs don't use "Arabic" numbers! Despite Western symbols being used worldwide,
in some parts of the world other sets of symbols co-exist for various purposes.
Here are Oriental numbers and a modem Arabic set.

Assuming our methods as in part a) above, calculate and translate:

to Modem Arabic;

to Basic Oriental.
Maida Waugh
Stuart, Florida
9. Related Groups
Difficulty: 4
a) How few people could make up a family of 1 daughter-in-law, 1 mother-in-law,
1 father-in-law, 2 daughters, 2 sons, 2 sisters, 1 brother, 3 grandchildren, 4 children,
2 mothers, 2 fathers, 1 grandfather, and 1 grandmother?
b) A class of 26 boys and 24 girls has 2 tracks: the college-prep crowd of 30
and a voc-training group. The college-bound proportion of boys to girls is the same
as girls to boys in the vocational group.
How many more boys are college-bound than girls noncollege?
c) Remember this oldie? One man describing another:
"Brothers and sisters have I none, but this man's father is my father's son."
What is their relationship?
Fred Rowe
Lighthouse Point, Florida
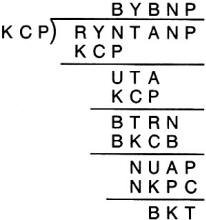 10. Insolvency and Equality 10. Insolvency and Equality
Difficulty: 4
a) When the ten letters in this puzzle are arranged in order from 1 to 0, what
do they spell?
b) What two numbers have the same sum and same anagram as another pair
of different numbers?
Mrs. Harry J. Graham
Ambler, Pennsylvania
11. Divide and Conquer
Difficulty: 4
If the prime factors of 28 are 1, 2, 2, and 7, how many prime factors has the
number 2,095,632,000?
E. S. Clymer, Jr.
Adelaide, South Australia
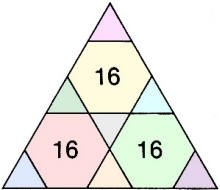 12. Magic Digits 12. Magic Digits
Difficulty: 5
a) Place the numbers 1-7 in the triangles so that the 4 triangles touching each
hexagon will add up to the number in the hexagon. Use each number 1-7 only once.
Rich Latta
Plainfield, Illinois
 b) Abbreviations for four consecutive years
beginning with '85 are inserted into the number square below. Fill the 12 empty
spaces with the numbers 6-17 so that each row, column, and corner-to-corner diagonal
will total exactly the same. b) Abbreviations for four consecutive years
beginning with '85 are inserted into the number square below. Fill the 12 empty
spaces with the numbers 6-17 so that each row, column, and corner-to-corner diagonal
will total exactly the same.
Josephine Belknap
Knoxville, Iowa
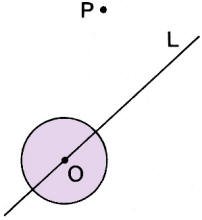 13. Flaring the Circle 13. Flaring the Circle
Difficulty: 5
Given: An unsealed straightedge, but no compass; pencil; infinite straight line
L; circle O centered on L; and point P not on any line, not in the circle.
Construct: A perpendicular from P to line L.
Don Scholten
Warner, New Hampshire
14. Madam, I'm Adam
Difficulty: 5
A palindrome is something reading
the same forward and backward. Analogously there are palindromic numbers, e.g.:
33, or 72827. It is postulated that every whole number (except those evenly divisible
by 10) has some multiples which are palindromes. In fact, an infinity of them.
Thus, there is a minimum palindromic multiple ("mipim") of any particular number.
What, then, is the highest mipim in the number series 1 to 100?
Dick Collier
Watervliet, New York
 15. Rectangle Ranch 15. Rectangle Ranch
Difficulty: 5
A certain Texas spread is rectangular and flat. Its dimensions and clues in no
particular order:
A) Short side of the rectangle in feet
B) Long side of the rectangle in yards
C) Perimeter of the rectangle in miles
D) Half of the diagonal of the rectan-gle in rods
E) One-third of the area of the rectangle in acres
F) The year of this OFA
G) One of the numbers is the sum of the 21 digits, but this isn't it.
There are no leading zeros, decimal points, fractions, or Earth curvature to
worry about.
Robert Lodge
Seattle, Washington
***
Answers to Old and New Mathematical Puzzles
 1. Two possibilities: ---> 1. Two possibilities: --->
2. $21,474,836.47 total, having saved over half on the 31st!
3. Impossible, even for a nonclosed line crossing itself.
4. 4 cows, 6 sheep, and 90 pigs.
5. The goose, 12 days after OFA publication.
6. 5.
7. a) 1970.
b) Doug, by 1 extra (Leap Year) day.
c) 96, probably. (>95, <124)
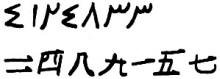 8. a) 1617 8. a) 1617
401
20179
b) --->
9. a) 7. A boy and 2 little girls, their father and mother and their father's
father and mother.
b) 6.
c) Speaker is the other man's father.
10. a) BANKRUPTCY
b) ELEVEN + TWO TWELVE + ONE
11. 19: 1, 27, 35, 53, 72, &
11.
12-15. Prize Set. See instructions on page 196.
Posted March 12, 2024
|








 3. Cross Only Once
3. Cross Only Once