 [Index] [Index]
Reproduced here are various Mathematical Puzzles from
The Old Farmer's Almanac,
published continuously since 1792. All copyrights hereby acknowledged.
|
The 1990 edition of the Old Farmer's
Almanac (OFA) had a pretty good set of "Old and New Mathematical Puzzles." Up until
around the late 1960s, some of the puzzles were very esoteric, often requiring one
be privy to certain standards or norms. Some were downright weird. Beginning around
2005, the OFA editors sometimes omitted the puzzles altogether or only included
simple ones, so as not to harm anyone's feelings if he/she couldn't figure it out
(seriously). Puzzles are rated for difficulty levels 1 through 5, with 5 being the
hardest. Solutions are provided for up through difficulty level 4. Sometimes, difficulty
level 5 problems are harder because they require a lot of guesses and iterations
to arrive at a solution. Other times, they require someone with the brilliance of
Euclid or Pythagoras, such as is the case with this year's puzzle number 15. Yikes.
Old and New Mathematical Puzzles
Blanton C. Wiggin, Puzzle Editor
Here are 15 classical, original, and timely puzzles for 1990 from our readers.
There should be something to interest everyone, and we hope they are challenging.
Everyday common sense and a little agility are all you'll need; you won't need calculus,
computers, alertness to tricks, or specialized knowledge, though these are sometimes
helpful. Some puzzles may require a chart or data from your local library.
We will award one prize of $50 for the best set of solutions to puzzles 12 through
15 received before February 1, 1990. The answers to these four are omitted here.
We use a point system to judge the prize set. A basic, unadorned, correct answer
is 20 points. For a thorough analysis, an elegant or novel answer, up to 5 points
extra. Numerical errors lose only 2 or 3 points, if it is clear that the method
is understood.
Explanations and Prize-Set Answers will be sent after June 15 to anyone sending
50¢ and a self-addressed stamped envelope to "Puzzle Answers," The Old Farmer's
Almanac, Dublin, NH 03444.
We will also pay $15 for any original puzzles we use in The Old Farmer's Almanac
for 1991. Closing date for submissions is February 1, 1990. Entries become the property
of Yankee Publishing Incorporated and cannot be acknowledged or returned.
We are happy to find that a number of teachers, grades 4 through college, use
our puzzles in their classrooms. We've enjoyed talking to some of these college
classes. Some of this year's puzzles submitted by students are noted.
The 1989 winner is Dick Collier educational administrator and former winner,
from Watervliet, New York, 97 points; followed by Emma Lou Henning, Vallejo, California,
and Robert L. Henderson, Belleville, Michigan, third. Fourth was Donald Chesley,
Valley Stream, Long Island. We appreciate the hard work and good answers from many
other contestants, and we have enjoyed the nice letters. Congratulations to all!
Copies of prize-set puzzles and answers for recent years may be obtained from
The Old Farmer's Almanac for $1 and a one-ounce stamp for each year requested; a
self-addressed envelope should be included.
Have fun with these 1990 puzzles, and send your answers early for puzzles 12-15.
Please use a separate sheet for each puzzle or answer. Be sure to put your name
and address on each sheet. Good luck!
Answers appear on page 219.
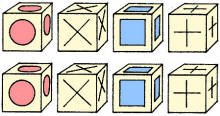
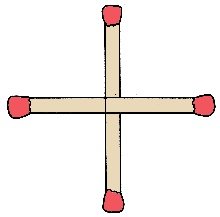 1. Squares & Cubes 1. Squares & Cubes
Difficulty: 1
 a) Can you make a square by moving
only 1 of these 4 paper matches? a) Can you make a square by moving
only 1 of these 4 paper matches?
b) How many different large cubes can you assemble from these 8 small cubes into
various arrangements so that each face of the large cube includes all four patterns?
Donal Drew, Standish, Maine
2. Innumeracy
Difficulty: 1
Illiteracy has been in the news a lot in recent years. Now it's illiteracy's
cousin, innumeracy. A lot of mathematics is simply having a good idea of reasonableness,
of size, or whether someone's statement makes sense.
All developers and engineers go through series of estimates, getting more precise
as projects develop.
Chances are you aren't innumerate, or you wouldn't be reading this. But test
yourself on these statements for fun!
a) "California is the most populous state and thus the most crowded."
b) "We expect to sell 200 million high-definition TV sets in 1991 and every year
thereafter."
c) "We won't need many: Using only one a minute, 500,000 will last for years."
d) "It took him a light-year to do it!"
e)"One hundred tons of fill will cover this acre a foot deep."
f) "We'll make twice as many of the mid-range of sizes as of the large or small."
Chandler Burpee
Goffstown. New Hampshire
3. Shortest Bridges
Difficulty: 2
a) A Dutch pasture is completely surrounded by a drainage ditch 20' wide filled
with water. During the 1953 ramp-storm, the farmer's bridge was destroyed. Among
the debris were two 19' planks, but no boats. How did the farmer solve the problem
of reaching his field?
b) When America's first canal was planned in South Hadley, Massachusetts, in
1790, it would separate two brothers' farmhouses. Where would a bridge have been
located, perpendicular to the straight, parallel canal banks, for minimum walking
distance between the houses?
Jeanne Campbell
Magna, Utah
4. Arithmetic Arrangements
Difficulty: 2
In how many different ways can one a) affix $6.43 exact postage, using only old
17¢ and 20¢ stamps?
Sidney Kravitz
Dover, New Jersey
b) arrange the digits 1 to 5 to fit this equation:
-- + -- + - =8
Rich Latta
Plainfield, Illinois
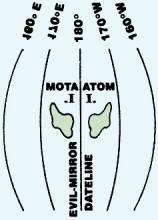 5. Meridian Mike 5. Meridian Mike
Difficulty: 2
Meridian Mike lives on Mirrored Planet, on small Atom Island near longitude 180·,
known also as the Evil-Mirror Date-line. An Evil Dictator rules. The eastern part
is densely populated and the Dictator has banned travel in any easterly direction.
Mike wanted to visit cousins living on Mota Island. As he sailed toward the Evil
Dateline, he realized that as soon as he crossed, he would be traveling east, which
was forbidden. Can Mike get to Mota Island legally? If so, how? And if not, how
will he get home?
Edward St. Jean, South Portland, Maine
6. A Long Wedge
Difficulty: 3
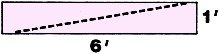 After sawing along one diagonal and
discarding one triangular section of board, where would you cut the remaining one
parallel to its end, to have 1 1/2 board feet in each piece? After sawing along one diagonal and
discarding one triangular section of board, where would you cut the remaining one
parallel to its end, to have 1 1/2 board feet in each piece?
Harland Carr, Northeast Harbor, Maine
7. River Float
Difficulty: 3
John started paddling steadily up the Connecticut in midstream at the Norwich
bridge. After 1 mile, he passed a floating bottle and continued at the same rate
for 12 minutes more.
Then he turned and paddled with the same effort downstream, passing the bottle
at the Norwich bridge.
How fast does the river flow?
Dr. Bill Mosenthal
Hanover, New Hampshire
8. Stretching Time
Difficulty: 3
The distance separating the tips of the hour and minute hands of a clock reaches
a maximum once each hour. Between 10 and 11 o'clock, when does this occur?
David A. Edgar
Hartford, Connecticut
9. Calendar Daze
Difficulty: 4
With American Senators elected for 6 years, on the first Tuesday after the first
Monday in November in even years, a man could win a regular election on his birthday
and then not face re-election as a first-term incumbent, either on his birthday
or the day before.
If so, when would his birthday be?
David Heber
San Diego, California
10. Numeri Mundum Regunt
Difficulty: 4
a) What is the next number in the series 0, 3, 20, 119,696, 4059?
b) Is there a relationship between these numbers?
Harvey Vigour
Waynesboro, Virginia
c) An old Mesopotamian numerologist's rule for prime numbers is:
P = 9n2 - 489n + 6683
Is this the long-sought magic sieve?
Sidney Kravitz
Dover, New Jersey
11. The Night Before Christmas
Difficulty: 4
Good that the longest nights of the year in the populous Northern Hemisphere
are at Christmastime. Santa can first visit those few towns above the Arctic Circle
where it is perpetually dark, ahead of time, and then start on . Christmas Eve,
at the first sunset below the circle, working the dark side of the Earth till the
last place sees the Christmas morning Sun. This 1990 tour is particularly favorable:
Not only is Cassiopeia capping Polaris and Betelgeuse above Bethlehem, but Santa
will also be guided on high by Saturn, Jupiter, and the Earth's northern halo.
Can you answer some of Red Nose's questions?
a) In the World view, where should he guide Santa? Where does the Sun set first
on Christmas Eve? And where does the Christmas Sun rise last?
b) Too wide a scope? OK, then, what state/province and town has the earliest
sunset Christmas Eve, and what town sees the Sun last Christmas morning?
c) By the way, how long is Christmas Eve?
Desmond Morin
Toronto, Ontario
12. Clock in the Sky
Difficulty: 5
Last year many readers realized that the Pointer Stars, Dubhe and Merak, of the
Big Dipper, are, at times, the hour hand of a conventional clock centered on the
Pole Star. At least once a night, they show true time. Develop some steps, or a
simple formula, that will convert their position at any time to correct clock time.
Fritz Geller
Keene, New Hampshire
13. Cross Numbers
Difficulty: 5
Construct a cross-number puzzle on a 6x6 grid with the following conditions:
There are six blanks, no two in the same row, column, or diagonal.
Each digit is used exactly three times with no leading zeros.
The smallest horizontal composite number is the year of this OFA.
Each 4-digit composite has a 3-digit prime factor in the puzzle and each 5-digit
composite has a 2-digit prime factor in the puzzle. The same prime number may be
used to factor more than one composite.
Robert L. Henderson
Belleville, Michigan
 14. Tangram Tiling 14. Tangram Tiling
Difficulty: 5
Can you construct a chess- or checkerboard out of these 14 pieces?
August Schilling and Frank Smith
Laguna Hills, California
15. Beaulieu Trisection
Difficulty: 5
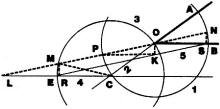 For 2 1/2 millennia, students have
had fun trying to construct three things posed by the Greeks: 1) a square whose
area equals a given circle, 2) a cube twice the volume of another, and perhaps most
popularly, 3) an angle measuring 1/3 of another. For 2 1/2 millennia, students have
had fun trying to construct three things posed by the Greeks: 1) a square whose
area equals a given circle, 2) a cube twice the volume of another, and perhaps most
popularly, 3) an angle measuring 1/3 of another.
One is allowed only an unmarked straightedge, a compass (and pencil) and is not
allowed to use both together to "verge," or to transfer lengths with the straightedge.
Of late, there are rigorous mathematics establishing the impossibility of all three.
Nevertheless, people keep trying. Here is a very subtle effort at trisecting the
angle. What is its fallacy? Please explain.
|
Given: Any angle AOB.

O. F Beaulieu, Richland, Washington
|
Proof:

|
Answers to Old and New Mathematical Puzzles
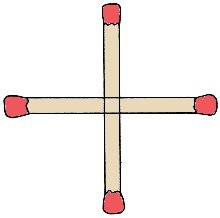 1. a. Slide one match slightly right. 1. a. Slide one match slightly right.
b. Only 1. Others are merely rotations, not different.
2. a. Hardly the most crowded, due to large size.
b. 10 million would be high for starters!
c. Not even a year; only 347 days!
d. A light-year is a certain distance, not time.
e. Less than 3/8" deep, if fill averages about 13 cubic feet/ton.
f. Reasonable; range of sizes of most things is bell-shaped.
 3. a. He put boards across corner of ditch. 3. a. He put boards across corner of ditch.
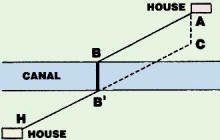 b. At BB' so HB' parallels
BA. b. At BB' so HB' parallels
BA.
4. a. One way only: 19 x 17¢ plus 16 x 20¢ stamps total $6.43.
b. One way only: 52 ÷ 13 + 4 = 8.
5. He travels to either pole, then follows the correct meridian down to the cousins.
6. 21.09" from square end.
7. 2.5 mph,
8. 10:21 9/11 o'clock.
9. November 2nd.
10.a. 23660. These are the lower of pairs of consecutive integers, whose squares,
summed, equal a perfect square. E.g.: 3, 4 & 5; 20, 21 & 29.
b. n3 = 6n2 + 2 - n1
c. Only up through n = 40.
11. a. Earliest sunset December 24 is in Eastern Siberia, and the latest sunrise
December 25 is north of Nome, Alaska. (Details on request; please send SASE.)
b. In the 60 states and provinces:
Baffin Island, NWT, or (if strictly provincial) Button Islands, Quebec, has the
earliest sunset. The latest sunrise is still north of Nome, Alaska. c. If Christmas
Eve be December 24: 48 hours, of course, just like any other day! If Christmas Eve
be only the night, Santa can still work almost 48 hours before dawn Christmas mom.
12-15. Prize Set. See Instructions on page 198.
Posted July 8, 2024
|







 1. Squares & Cubes
1. Squares & Cubes 

 After sawing along one diagonal and
discarding one triangular section of board, where would you cut the remaining one
parallel to its end, to have 1 1/2 board feet in each piece?
After sawing along one diagonal and
discarding one triangular section of board, where would you cut the remaining one
parallel to its end, to have 1 1/2 board feet in each piece? 



 1. a. Slide one match slightly right.
1. a. Slide one match slightly right. 3. a. He put boards across corner of ditch.
3. a. He put boards across corner of ditch.

