July 1932 Radio News
 [Table
of Contents] [Table
of Contents]
Wax nostalgic about and learn from the history of early
electronics. See articles from
Radio & Television News, published 1919-1959. All copyrights hereby
acknowledged.
|
I challenge you to find a calculus
lesson in a modern-day electronics magazine. In 1932, not all that long after Isaac
Newton developed differential calculus (that's a joke), Radio News magazine
ran a series of "Mathematics in Radio" articles that included, among other topics,
a few lessons in calculus. Anyone who has taken college-level science or engineering
courses knows how indispensible calculus is in working out many circuit, physics,
and chemistry problems. My appreciation for calculus came when I realized that it
actually allowed me to derive the kinds of standard equations that are commonly
seen in lower level applications. For instance, if you needed to know the
volume
of a sphere, you could look up the familiar Volume = 4/3 π r3
formula, or you could write the equation
Volume =
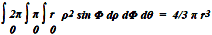
Area, mass, center of mass, and length of a spiral line, are other examples of
problems that can be solved by knowing the fundamental mathematics behind the equations.
See also
National
Radio Institute advertisement, December 1954 Radio News;
Mathematics
in Radio in July 1932 Radio News;
Measuring Inductance and Capacity, June 1931 Radio-Craft;
Mathematics in Radio,
March 1933 Radio News;
Radio Frequencies and Their Allocation, June | July 1940 National Radio
News;
Your Radio Training and the Defense Program, December 1940 | January 1941
National Radio News.
Mathematics in Radio
Calculus and its Application in Radio - Part Seventeen
By J. E. Smith*
In order to apply the formulas for differentiating, the student should become
familiar with the following examples with reference to the standard forms (1)-(5)
inclusive (which were shown in the last lesson+).
Differentiate the following:
1) y = x4
Here, formula (5) applies where x = v, and the exponent 4 = u.
Solution:
(A) 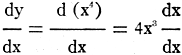 , but from the formula
(1), dx/dx = 1, , but from the formula
(1), dx/dx = 1,
therefore A becomes: dy/dx = 4x3 (answer).
2) y = x6
3) y = x2
4) y = x9
5) y - x5
6) y = ax3 + bx5
Here, formulas (3) and (5) apply, where a and b = c of formula (3), and the exponents
3 and 5 respectively = n.
Solution:
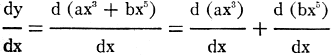 = 3ax2
+ 5bx4 (answer). = 3ax2
+ 5bx4 (answer).
7) y = ax4
8) y = ax6 + bx2
9) y = ax7 - x6
10) y - ax3 - bx3
11) y = 5x4 + 3x2 - 6
The derivative of a constant is zero; i.e., dc/dx = 0.
Solution:
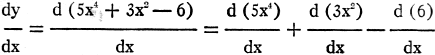 = 20x3
+ 6x (answer). = 20x3
+ 6x (answer).
|
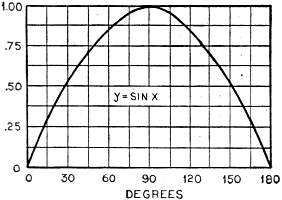
Figure 1
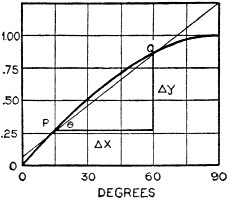
Figure 2
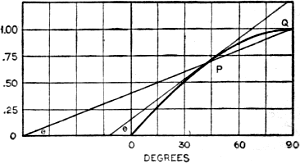
Figure 3
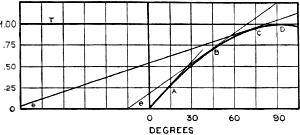
Figure 4
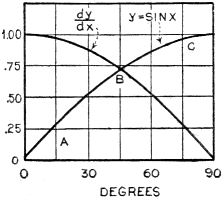
Figure 5
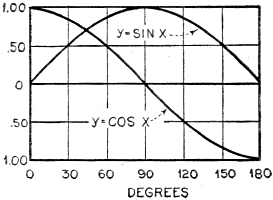
Figure 6
|
12) y = 3cx2 - 8dx + 5e
13) y = 2ax2 + 4dx2 - 5ax
The sinusoidal functions are those expressed by the sine and cosine curves as
well as those functions which are closely allied to them, which are the tangent
and cotangent curves so important in geometry.
Electrical and radio theory are very often advanced by the use of calculus, which
takes the liberty of performing the necessary operations on the sine and cosine
functions. Let us apply the theory which was outlined above in finding the derivative
of a sine function. That is, if a sine function is expressed by y = sin x, it is
the purpose of this analysis to determine its proper derivative.
In the previous texts it has been shown how to plot the function y = sin x, and
this is shown in Figure 1 for the values of x from 0-180 degrees. In order to study
the derivative of this function, reference is made to Figures 2 and 3, where the
values of x have been plotted from 0-90 degrees. Applying the theory which has been
outlined above, we see that when Δx approaches zero, Δy/Δx finally
approaches a limiting value, and it is remembered that this limiting value is called
the derivative of y with respect to x, This limit, represented by dy/dx, has been
shown above to be equal to the tangent θ.
With reference to Figure 4, it is noticed that the angle θ at the point A is
somewhat larger than the values of θ for the points Band C. Finally, at the point
D, the tangent line TD becomes parallel to the abscissa, and it is noticed that
the angle θ has become increasingly smaller until it has approached the value of
zero.
Now, the derivative of the function y = sin x at the point A is by definition
equal to the tangent of θ. In like manner, the derivatives of the function at points
B, C and D are again equal respectively to the tangents of the angles θ.
By close analysis of the relative sizes of these angles, we arrive at the following
table:
For point A, θ equals about 45°
For point B, θ equals about 35°
For point C, θ equals about 17°
For point D, θ equals about 0°
But the tangent of these angles is by definition equal to the derivative of the
function at its respective points; thus:
dy/dx at point A is about 1
dy/dx at point B is about 0.70
dy/dx at point C is about 0.31
dy/dx at point D is about 0
Plotting these values of dy/dx at point A, B and C, respectively, we have the
graph of Figure 5. But this dy/dx curve is further noticed to be the same as the
function y = cos x, so it is apparent that:
d (sin x)/ax = cos x
or the derivative of the sin x is equal to the cos x.
Figure 6 shows the functions y = sin x and y = cos x plotted together.
Formulas for Differentiating Standard Forms
The following formulas are a continuation of the ones listed above from (1-5)
inclusive.
6. d/dx (sin v) = cos v (dv/dx)
The derivative of a sine function is equal to its cosine function, times the
derivative of the function.
7. d (cos v) / dx = -sin v (dv/dx)
8. d (tan v) / dx = sec2 v (dv/dx)
9. d (cot v) / dx = -csc2 v (dv/dx)
See v and csc v above are the abbreviations for secant and cosecant, respectively.
The application of the above differential forms to radio theory is now quite readily
presented.
Answers to Problems:
1) 4x3
2) 6x5
3) 2x
4) 9x8
5) 5x4
6) 3ax2 + 5bx4
7) 4ax3
8) 6ax5 + 2bx
9) 7ax6 - 6x5
10) 1 - 3ax2 - 3bx2
11) 20x3 + 6x
12) 6cx - 8d
13) 4ax + 8x - 5a
*President National Radio Institute.
+Note - Many of the examples have been taken from the book, "Elements of the
Differential and Integral Calculus," by W. A. Granville, published by Ginn and Company,
N. Y.
Posted April 27, 2023
(updated from original post
on 8/22/2013)
|









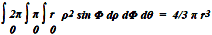
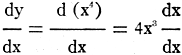 , but from the formula
(1), dx/dx = 1,
, but from the formula
(1), dx/dx = 1, 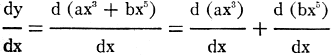 = 3ax2
+ 5bx4 (answer).
= 3ax2
+ 5bx4 (answer). 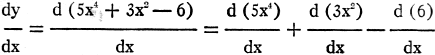 = 20x3
+ 6x (answer).
= 20x3
+ 6x (answer). 





