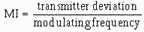Module 12 - Modulation Principles
Pages i,
1-1,
1-11,
1-21,
1-31,
1-41,
1-51,
1-61,
1-71,
2-1,
2-11,
2-21,
2-31,
2-41,
2-51,
2-61,
3-1,
3-11,
3-21,
3-31, AI-1, Index, Assignment 1, 2
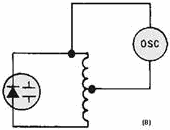
Figure 2-15B. - Varactor symbol and schematic. SIMPLIFIED Circuit.
Notice the simplicity of operation of the circuit in figure 2-16. An AF signal that is applied to the input
results in the following actions: (1) On the positive alternation, reverse bias increases and the dielectric
(depletion region) width increases. This decreases capacitance which increases the frequency of the oscillator.
(2) On the negative alternation, the reverse bias decreases, which results in a decrease in oscillator frequency.
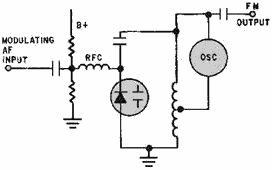
Figure 2-16. - Varactor FM
modulator.
Many different FM modulators are available, but they all use the basic principles you have just studied.
The main point to remember is that an oscillator must be used to establish the reference (carrier) frequency.
Secondly, some method is needed to cause the oscillator to change frequency in accordance with an AF signal.
Anytime this can be accomplished, we have a frequency modulator. Q-7. How does the reactance-tube
modulator impress intelligence onto an RF carrier? Q-8. What characteristic of a transistor is varied in
a semiconductor-reactance modulator? Q-9. What circuit section is required in the output of a
multivibrator modulator to eliminate unwanted output frequencies? Q-10. What characteristic
of a varactor is used in an FM modulator?
2-21
Phase MODULATION Frequency modulation requires the oscillator frequency to
deviate both above and below the carrier frequency. During the process of frequency modulation, the peaks of each
successive cycle in the modulated waveform occur at times other than they would if the carrier were unmodulated.
This is actually an incidental phase shift that takes place along with the frequency shift in fm. Just the
opposite action takes place in phase modulation. The AF signal is applied to a Phase Modulator in pm. The
resultant wave from the phase modulator shifts in phase, as illustrated in figure 2-17. Notice that the time
period of each successive cycle varies in the modulated wave according to the audio-wave variation. Since
frequency is a function of time period per cycle, we can see that such a phase shift in the carrier will cause its
frequency to change. The frequency change in FM is vital, but in pm it is merely incidental. The amount of
frequency change has nothing to do with the resultant modulated wave shape in pm. At this point the comparison of
FM to pm may seem a little hazy, but it will clear up as we progress.
Figure 2-17. - Phase modulation. Let's review some voltage phase relationships. Look at figure 2-18 and compare the three voltages (A, B,
and C). Since voltage a begins its cycle and reaches its peak before voltage B, it is said to lead voltage B.
Voltage C, on the other hand, lags voltage B by 30 degrees. In phase modulation the phase of the carrier is caused
to shift at the rate of the AF modulating signal. In figure 2-19, note that the unmodulated carrier has constant
phase, amplitude, and frequency. The dotted wave shape represents the modulated carrier. Notice that the phase on
the second peak leads the phase of the unmodulated carrier. On the third peak the shift is even greater; however,
on-the fourth peak, the peaks begin to realign phase with each other. These relationships represent the effect of
1/2 cycle of an AF modulating signal. On the negative alternation of the AF intelligence, the phase of the carrier
would lag and the peaks would occur at times later than they would in the unmodulated carrier.
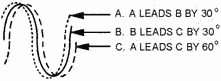
Figure 2-18. - Phase relationships. 2-22
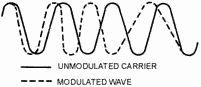
Figure 2-19. - Carrier with and without modulation. The presentation of these two waves together does not mean that we transmit a modulated wave together
with an unmodulated carrier. The two waveforms were drawn together only to show how a modulated wave looks when
compared to an unmodulated wave. Now that you have seen the phase and frequency shifts in both FM and pm,
let's find out exactly how they differ. First, only the phase shift is important in pm. It is proportional to the
AF modulating signal. To visualize this relationship, refer to the wave shapes shown in figure 2-20. Study the
composition of the FM and pm waves carefully as they are modulated with the modulating wave shape. Notice that in
fm, the carrier frequency deviates when the modulating wave changes polarity. With each alternation of the
modulating wave, the carrier advances or retards in frequency and remains at the new frequency for the duration of
that cycle. In pm you can see that between one alternation and the next, the carrier phase must change, and the
frequency shift that occurs does so only during the transition time; the frequency then returns to its normal
rate. Note in the pm wave that the frequency shift occurs only when the modulating wave is changing polarity. The
frequency during the constant amplitude portion of each alternation is the REST Frequency. 
Figure 2-20. - PM versus FM. The relationship, in pm, of the modulating AF to the change in the phase shift is easy to see once you
understand AM and FM principles. Again, we can establish two clear-cut rules of phase modulation: 2-23
• AMOUNT of Phase SHIFT Is PROPORTIONAL to The Amplitude of The MODULATING Signal. (If a 10-volt
signal causes a phase shift of 20 degrees, then a 20-volt signal causes a phase shift of 40 degrees.) •
RATE of Phase SHIFT Is PROPORTIONAL to The Frequency of The MODULATING Signal. (If the carrier were modulated with
a 1-kilohertz tone, the carrier would advance and retard in phase 1,000 times each second.) Phase
modulation is also similar to frequency modulation in the number of sidebands that exist within the modulated wave
and the spacing between sidebands. Phase modulation will also produce an infinite number of sideband frequencies.
The spacing between these sidebands will be equal to the frequency of the modulating signal. However, one factor
is very different in phase modulation; that is, the distribution of power in pm sidebands is not similar to that
in FM sidebands, as will be explained in the next section.
Modulation Index Recall from frequency modulation that modulation index is used to
calculate the number of significant sidebands existing in the waveform. The higher the modulation index, the
greater the number of sideband pairs. The modulation index is the ratio between the amount of oscillator deviation
and the frequency of the modulating signal:
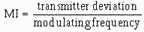
In frequency modulation, we saw that as the frequency of the modulating signal increased (assuming the
deviation remained constant) the number of significant sideband pairs decreased. This is shown in views (A) and
(B) of figure 2-21. Notice that although the total number of significant sidebands decreases with a higher
frequency-modulating signal, the sidebands spread out relative to each other; the total bandwidth increases. 2-24
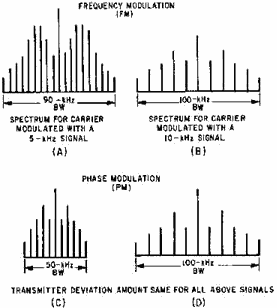
Figure 2-21. - FM versus pm spectrum distribution. In phase modulation the oscillator does not deviate, and the power in the sidebands is a function of the
amplitude of the modulating signal. Therefore, two signals, one at 5 kilohertz and the other at 10 kilohertz, used
to modulate a carrier would have the same sideband power distribution. However, the 10-kilohertz sidebands
would be farther apart, as shown in views (C) and (D) of figure 2-21. When compared to fm, the bandwidth of the pm
transmitted signal is greatly increased as the frequency of the modulating signal is increased. As we pointed
out earlier, phase modulation cannot occur without an incidental change in frequency, nor can frequency modulation
occur without an incidental change in phase. The term FM is loosely used when referring to any type of angle
modulation, and phase modulation is sometimes incorrectly referred to as "indirect fm." This is a definition that
you should disregard to avoid confusion. Phase modulation is just what the words imply - phase modulation of a
carrier by an AF modulating signal. You will develop a better understanding of these points as you advance in your
study of modulation. Basic Modulator In phase modulation you learned that varying the
phase of a carrier at an intelligence rate caused that carrier to contain variations which could be converted back
into intelligence. One circuit that can cause this phase variation is shown in figure 2-22. 2-25
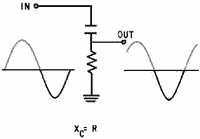
Figure 2-22. - Phase shifting a sine wave. The capacitor in series with the resistor forms a phase-shift circuit. With a constant frequency RF
carrier applied at the input, the output across the resistor would be 45 degrees out of phase with the input if XC
= R.
Now, let's vary the resistance and observe how the output is affected in figure 2-23. As the resistance
reaches a value greater than 10 times XC, the phase difference between input and output is nearly 0 degrees. For
all practical purposes, the circuit is resistive. As the resistance is decreased to 1/10 the value of XC, the
phase difference approaches 90 degrees. The circuit is now almost completely capacitive. By replacing the resistor
with a vacuum tube, as shown in view (A) of figure 2-24, we can vary the resistance (vacuum-tube impedance) by
varying the voltage applied to the grid of the tube. The frequency applied to the circuit (from a
crystal-controlled master oscillator) will be shifted in phase by 45 degrees with no audio input [view (B)]. With
the application of an audio signal, the phase will shift as the impedance of the tube is varied.
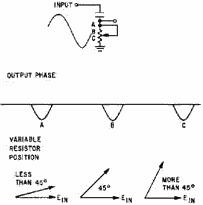
Figure 2-23. - Control over the amount of phase shift. 2-26
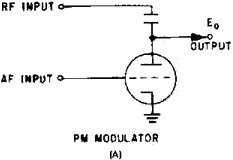
Figure 2-24A. - Phase modulator. 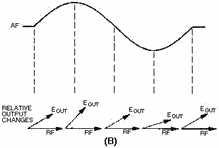
Figure 2-24B. - Phase modulator. In practice, a circuit like this could not provide enough phase shift to produce the desired results in
the output. Several of these circuits are arranged in cascade to provide the desired amount of phase shift. Also,
since the output of this circuit will vary in amplitude, the signal is fed to a limiter to remove amplitude
variations.
The major advantage of this type modulation circuit over frequency modulation is that this circuit uses a
crystal-controlled oscillator to maintain a stable carrier frequency. In FM the oscillator cannot be crystal
controlled because it is actually required to vary in frequency. That means that an FM oscillator will require a
complex automatic frequency control (AFC) system. An AFC system ensures that the oscillator stays on the same
carrier frequency and achieves a high degree of stability. The AFC circuit will be covered in a later module.
Phase-Shift Keying Phase-shift keying (PSK) is similar to ON-ofF CW keying in AM systems and
frequency-shift keying in FM systems. PSK is most useful when the code elements are all of equal length; that is,
all marks and spaces, whether message elements or synchronizing signals, occupy identical elements of time. It is
not fully suitable for use on start-stop teletypewriter circuits where the stop pulse is 1.42 times longer than
the 2-27
other pulses. Neither is it applicable to those pulsed systems in which the duration or position of
the pulses are varied by the modulation frequency. In its simplest form, PSK operates on the principle of phase
reversal of the carrier. Each time a mark is received, the phase is reversed. No phase reversal takes place when a
space is received. In binary systems, marks and spaces are called ONES and ZEROS, respectively, so that a ONE
causes a 180-degree phase shift, and a ZERO has no effect on the incoming signal. Figure 2-25 shows the
application of phase-shift keying to an unmodulated carrier [view (A)] in the AF range. For transmission over
other than a conductive path, the wave shown in view (D) must be used as the modulating signal for some other
system of modulating an RF carrier.

Figure 2-25A. - Phase-shift keying. UNMODULATED CARRIER. 
Figure 2-25B. - Phase-shift keying. MODULATION Signal - DATA ELEMENTS. 
Figure 2-25C. - Phase-shift keying. MODULATED CARRIER. 
Figure 2-25D. - Phase-shift keying. MODULATED CARRIER AFTER FILTERING. The modulating signal in view (B) consists of a bit stream of ZEROS and ONES. a ZERO does not affect the
carrier frequency which is usually set to equal the bit rate. For example, a data stream of 1,200 bits per second
would have a carrier of 1,200 hertz. When a data bit ONE occurs, the phase of the carrier frequency is shifted 180
degrees. In view (C) we find that the third, fifth, and sixth cycles (all ONE) have been reversed in phase. This
phase reversal produces CUSPS (sharp phase reversals) which are usually 2-28
removed by filtering before transmission or further modulation. This filtering action limits the
bandwidth of the output signal frequencies. The resulting wave is shown in view (D). The exact waveform of
figure 2-25, view (D), can be obtained by logic operations of timing and data. This is illustrated in figure 2-26,
where a timing signal [view (A)] is used rather than a carrier frequency. The data (intelligence) is shown in view
(B) and is combined with the timing signal to produce a combination digital modulation signal, as shown in view
(C). The square-wave pattern of the digital modulation is filtered to limit the bandwidth of the signal
frequencies, as shown in view (D). This system has been used in some high-speed data equipment, but it offers no
particular advantage over other systems of modulation, particularly the pulse-modulated systems for high-speed
data transmission. Q-11. What type of modulation depends on the carrier-wave phase shift?
Q-12. What components may be used to build a basic phase modulator? Q-13. Phase-shift keying is similar
to what other two types of modulation?

Figure 2-26A. - Simulated phase-shift keying. TIMING. 
Figure 2-26B. - Simulated phase-shift keying. DATA. 
Figure 2-26C. - Simulated phase-shift keying. DIGITAL MODULATION. 
Figure 2-26D. - Simulated phase-shift keying. DIGITAL MODULATION AFTER FILTERING. 2-29
PULSE MODULATION Another type of modulation is PULSE MODULATION. Pulse modulation
has many uses, including telegraphy, radar, telemetry, and multiplexing. Far too many applications of pulse
modulation exist to elaborate on any one of them, but in this section we will cover the basic principles of pulse
modulation.
Characteristics Amplitude modulating a simple RF carrier to a point where it becomes
drastically overmodulated could produce a waveform similar to that required in pulse modulation. a modulating
signal [view (A) of figure 2-27 that is much larger than the carrier results in the modulation envelope shown in
view (B). The modulation envelope would be the same if the modulating wave shape were not sinusoidal; that is,
like the one shown in view (C).
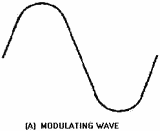
Figure 2-27A. - Overmodulation of a carrier. MODULATING WAVE. 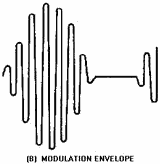
Figure 2-27B. - Overmodulation of a carrier. MODULATION ENVELOPE. 2-30
| - |
Matter, Energy,
and Direct Current |
| - |
Alternating Current and Transformers |
| - |
Circuit Protection, Control, and Measurement |
| - |
Electrical Conductors, Wiring Techniques,
and Schematic Reading |
| - |
Generators and Motors |
| - |
Electronic Emission, Tubes, and Power Supplies |
| - |
Solid-State Devices and Power Supplies |
| - |
Amplifiers |
| - |
Wave-Generation and Wave-Shaping Circuits |
| - |
Wave Propagation, Transmission Lines, and
Antennas |
| - |
Microwave Principles |
| - |
Modulation Principles |
| - |
Introduction to Number Systems and Logic Circuits |
| - |
- Introduction to Microelectronics |
| - |
Principles of Synchros, Servos, and Gyros |
| - |
Introduction to Test Equipment |
| - |
Radio-Frequency Communications Principles |
| - |
Radar Principles |
| - |
The Technician's Handbook, Master Glossary |
| - |
Test Methods and Practices |
| - |
Introduction to Digital Computers |
| - |
Magnetic Recording |
| - |
Introduction to Fiber Optics |
| Note: Navy Electricity and Electronics Training
Series (NEETS) content is U.S. Navy property in the public domain. |
|