|
[Go to TOC]
FREQUENCY / PHASEEFFECTS OF ANTENNAS
The radiation patterns of the antennas presented in the previous section are for antenna geometries most
commonly used. The antenna should be viewed as a matching network that takes the power from a transmission line
(50 ohm, for example), and matches it to the free space "impedance" of 377 ohms. The most critical parameter is
the change of VSWR with frequency. The pattern usually does not vary much from acceptable to the start of
unacceptable VSWRs (> 2:1). For a given physical antenna geometric size, the actual radiation pattern varies with
frequency.
The antenna pattern depicted in Figure 1 is for the dipole pictured in Section 3-3. The maximum gain is
normalized to the outside of the polar plot and the major divisions correspond to 10 dB change. In this example,
the dipole length (in wavelengths) is varied, but the same result can be obtained by changing frequency with a
fixed dipole length. From the figure, it can be seen that side lobes start to form at 1.258 and the side lobe
actually has more gain than the main beam at 1.58. Since the radiation pattern changes with frequency, the gain
also changes.
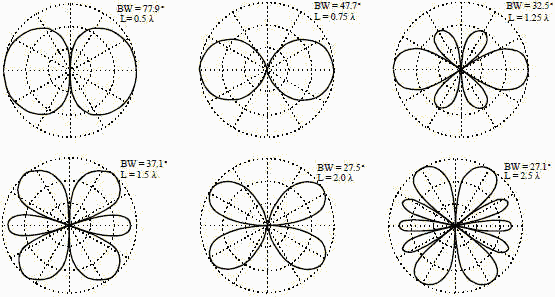
Figure 1. Frequency Effects
Figure 2 depicts phase/array effects, which are yet another method for obtaining varied radiation patterns. In
the figure, parallel dipoles are viewed from the end. It can be seen that varying the phase of the two
transmissions can cause the direction of the radiation pattern to change. This is the concept behind phased array
antennas. Instead of having a system mechanically sweeping the direction of the antenna through space, the phase
of radiating components is varied electronically, producing a moving pattern with no moving parts. It can also be
seen that increasing the number of elements further increases the directivity of the array. In an array, the
pattern does vary considerably with frequency due to element spacing (measured in wavelengths) and the frequency
sensitivity of the phase shifting networks.
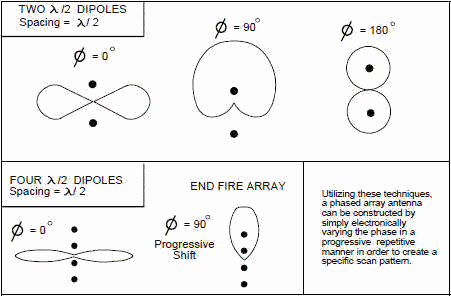
Figure 2. Phase / Array Effects
Figure 2 depicts phase/array effects, which are yet another method for obtaining varied radiation patterns. In the
figure, parallel dipoles are viewed from the end. It can be seen that varying the phase of the two transmissions
can cause the direction of the radiation pattern to change. This is the concept behind phased array antennas.
Instead of having a system mechanically sweeping the direction of the antenna through space, the phase of
radiating components is varied electronically, producing a moving pattern with no moving parts. It can also be
seen that increasing the number of elements further increases the directivity of the array. In an array, the
pattern does vary considerably with frequency due to element spacing (measured in wavelengths) and the frequency
sensitivity of the phase shifting networks. Two antennas that warrant special consideration are the phased
array and the Rotman bootlace type lens. Both of these antennas find wide application in EW, RADAR, and
Communications. The phased array will be described first. LINEAR PHASED ARRAY The
linear phased array with equal spaced elements is easiest to analyze and forms the basis for most array designs.
Figure 3 schematically illustrates a corporate feed linear array with element spacing d.
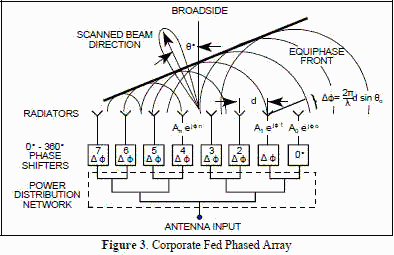 It
is the simplest and is still widely used. By controlling the phase and amplitude of excitation to each element, as
depicted, we can control the direction and shape of the beam radiated by the array. The phase excitation, ф(n),
controls the beam pointing angle, θo, in a phased array. To produce a broadside beam, θo=0, requires phase
excitation, ф(n)=0. Other scan angles require an excitation, N(n) = nkd sin(θo), for the nth element where k is
the wave number (2π/λ). In this manner a linear phased array can radiate a beam in any
scan direction, θo, provided the element pattern has sufficient beamwidth. The amplitude excitation, An, can be
used to control beam shape and sidelobe levels. Often the amplitude excitation is tapered in a manner similar to
that used for aperture antennas to reduce the sidelobe levels. One of the problems that can arise with a phased
array is insufficient bandwidth, since the phase shift usually is not obtained through the introduction of
additional path length. However, it should be noted that at broadside the corporate feed does have equal path
length and would have good bandwidth for this scan angle. It
is the simplest and is still widely used. By controlling the phase and amplitude of excitation to each element, as
depicted, we can control the direction and shape of the beam radiated by the array. The phase excitation, ф(n),
controls the beam pointing angle, θo, in a phased array. To produce a broadside beam, θo=0, requires phase
excitation, ф(n)=0. Other scan angles require an excitation, N(n) = nkd sin(θo), for the nth element where k is
the wave number (2π/λ). In this manner a linear phased array can radiate a beam in any
scan direction, θo, provided the element pattern has sufficient beamwidth. The amplitude excitation, An, can be
used to control beam shape and sidelobe levels. Often the amplitude excitation is tapered in a manner similar to
that used for aperture antennas to reduce the sidelobe levels. One of the problems that can arise with a phased
array is insufficient bandwidth, since the phase shift usually is not obtained through the introduction of
additional path length. However, it should be noted that at broadside the corporate feed does have equal path
length and would have good bandwidth for this scan angle.
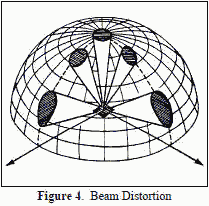 The
linear array described above would yield a narrow fan beam with the narrow beamwidth in the plane of the array. To
obtain a pencil beam it would be necessary to array several of these line arrays. A problem associated with all
electronic scanning is beam distortion with scan angle. Figure 4 illustrates this phenomenon. It results in spread
of the beam shape and a consequent reduction in gain known as "scan loss". For an ideal array element, scan loss
is equal to the aperture size reduction (projected) in the scan direction which varies as cos θ. The
linear array described above would yield a narrow fan beam with the narrow beamwidth in the plane of the array. To
obtain a pencil beam it would be necessary to array several of these line arrays. A problem associated with all
electronic scanning is beam distortion with scan angle. Figure 4 illustrates this phenomenon. It results in spread
of the beam shape and a consequent reduction in gain known as "scan loss". For an ideal array element, scan loss
is equal to the aperture size reduction (projected) in the scan direction which varies as cos θ. When
elements are spaced greater than λ/2 apart, grating lobes are possible when scanning. As the beam is scanned
further from broadside, a point is reached at which a second symmetrical main lobe is developed at the negative
scan angle from broadside. This condition is not wanted because antenna gain is immediately reduced by 3 dB due to
the second lobe. Grating lobes are a significant problem in EW applications because the broad frequency bandwidth
requirements mean that at the high end of the frequency band, the elements may be spaced greater than λ/2.
There are many other factors to consider with a phased array such as coning, where the beam curves at large scan
angles, and mutual coupling between elements that affect match and excitation. They will not be covered in detail
here. Of interest is the gain of the array which is given by:
 Where each element is as described in Section 3-4.
Where each element is as described in Section 3-4. Ge(θ) is the element gain which in this
case has been taken the same for all elements. Note that if we set A(n)=1, and ф(n)=0, then at broadside where
sin(θ) = 0, the gain would be (N Ge). This represents the maximum gain of the array, which typically will not
exceed nπ, and is a familiar figure.
 ROTMAN
BOOTLACE LENS ROTMAN
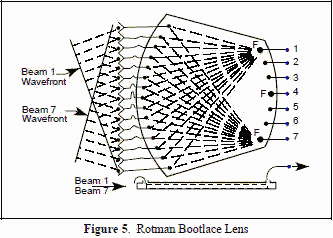
BOOTLACE LENS Another method of feeding an array of elements is to use a lens such as the Rotman
(rhymes with rotten) Bootlace type shown in Figure 5. The lens consists of a parallel plate region (nowadays
microstrip or stripline construction) and cables of specified length connecting the array of elements to the
parallel plate region. The geometry of the lens and the cable lengths are designed so that all ray paths traced
from a beam port on the right side to its associated wavefront on the left array port side, are equal. This
tailoring of the design is accomplished at three focus points (beam ports 1, 4, and 7 in Figure 5). Departure from
perfect focus at intermediate beam ports is negligible in most designs. The Rotman lens provides both true
time delay phase shift and amplitude taper in one lens component. The true time delay is one of the distinct
advantages of the lens over the phase shifted array since that makes it independent of frequency. To understand
how the taper is obtained requires knowledge of the parallel plate region. For a stripline design the unit would
consist of a large flat plate-like center conductor sandwiched between two ground planes, and having a shape much
like that of the plan view outline shown in Figure 5 with individual tapered launchers (connectors) attached to
each beam port and array port. If the antenna is in the receive mode, the energy intercepted on the array port
side can be controlled by the angle subtended by the tapered sections of the connector (launcher) much like a
larger antenna would intercept a larger portion of energy from free space.
Unlike the phased array with its fine beam steering, the Rotman lens provides only a distinct set of beams.
Fine steering is obtained by combining beams either equally or unequally to form intermediate beams. As can be
seen in Figure 6, this results in a broader beam with less gain but lower side lobes than the primary beams.
High transmit power can be obtained using a Rotman lens by placing a low power amplifier between each lens output
port and its antenna. In this case a separate Rotman lens would have to be used for receiving.
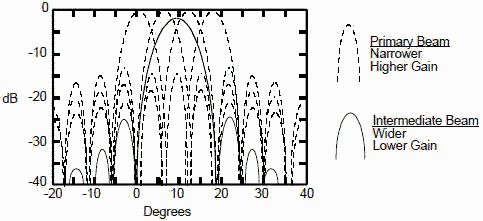
Figure 6. Primary and Intermediate Beam Formation in Lens Arrays
Table of Contents for Electronics Warfare and Radar Engineering Handbook
Introduction |
Abbreviations | Decibel | Duty
Cycle | Doppler Shift | Radar Horizon / Line
of Sight | Propagation Time / Resolution | Modulation
| Transforms / Wavelets | Antenna Introduction
/ Basics | Polarization | Radiation Patterns |
Frequency / Phase Effects of Antennas |
Antenna Near Field | Radiation Hazards |
Power Density | One-Way Radar Equation / RF Propagation
| Two-Way Radar Equation (Monostatic) |
Alternate Two-Way Radar Equation |
Two-Way Radar Equation (Bistatic) |
Jamming to Signal (J/S) Ratio - Constant Power [Saturated] Jamming
| Support Jamming | Radar Cross Section (RCS) |
Emission Control (EMCON) | RF Atmospheric
Absorption / Ducting | Receiver Sensitivity / Noise |
Receiver Types and Characteristics |
General Radar Display Types |
IFF - Identification - Friend or Foe | Receiver
Tests | Signal Sorting Methods and Direction Finding |
Voltage Standing Wave Ratio (VSWR) / Reflection Coefficient / Return
Loss / Mismatch Loss | Microwave Coaxial Connectors |
Power Dividers/Combiner and Directional Couplers |
Attenuators / Filters / DC Blocks |
Terminations / Dummy Loads | Circulators
and Diplexers | Mixers and Frequency Discriminators |
Detectors | Microwave Measurements |
Microwave Waveguides and Coaxial Cable |
Electro-Optics | Laser Safety |
Mach Number and Airspeed vs. Altitude Mach Number |
EMP/ Aircraft Dimensions | Data Busses | RS-232 Interface
| RS-422 Balanced Voltage Interface | RS-485 Interface |
IEEE-488 Interface Bus (HP-IB/GP-IB) | MIL-STD-1553 &
1773 Data Bus | This HTML version may be printed but not reproduced on websites.
|










 It
is the simplest and is still widely used. By controlling the phase and amplitude of excitation to each element, as
depicted, we can control the direction and shape of the beam radiated by the array. The phase excitation, ф(n),
controls the beam pointing angle, θo, in a phased array. To produce a broadside beam, θo=0, requires phase
excitation, ф(n)=0. Other scan angles require an excitation, N(n) = nkd sin(θo), for the nth element where k is
the wave number (2
It
is the simplest and is still widely used. By controlling the phase and amplitude of excitation to each element, as
depicted, we can control the direction and shape of the beam radiated by the array. The phase excitation, ф(n),
controls the beam pointing angle, θo, in a phased array. To produce a broadside beam, θo=0, requires phase
excitation, ф(n)=0. Other scan angles require an excitation, N(n) = nkd sin(θo), for the nth element where k is
the wave number (2 The
linear array described above would yield a narrow fan beam with the narrow beamwidth in the plane of the array. To
obtain a pencil beam it would be necessary to array several of these line arrays. A problem associated with all
electronic scanning is beam distortion with scan angle. Figure 4 illustrates this phenomenon. It results in spread
of the beam shape and a consequent reduction in gain known as "scan loss". For an ideal array element, scan loss
is equal to the aperture size reduction (projected) in the scan direction which varies as cos θ.
The
linear array described above would yield a narrow fan beam with the narrow beamwidth in the plane of the array. To
obtain a pencil beam it would be necessary to array several of these line arrays. A problem associated with all
electronic scanning is beam distortion with scan angle. Figure 4 illustrates this phenomenon. It results in spread
of the beam shape and a consequent reduction in gain known as "scan loss". For an ideal array element, scan loss
is equal to the aperture size reduction (projected) in the scan direction which varies as cos θ. Where each element is as described in Section 3-4.
Where each element is as described in Section 3-4. ROTMAN
BOOTLACE LENS
ROTMAN
BOOTLACE LENS
