|
[Go to TOC] ONE-WAY RADAR EQUATION / RF PROPAGATION
The one-way (transmitter to receiver) radar equation is derived in this section. This equation is most commonly used in RWR or ESM type
of applications. The following is a summary of the important equations explored in this section:

 Recall
from Section 4-2 that the power density at a distant point from a radar with an antenna gain of Gt is the power density from an isotropic
antenna multiplied by the radar antenna gain. Recall
from Section 4-2 that the power density at a distant point from a radar with an antenna gain of Gt is the power density from an isotropic
antenna multiplied by the radar antenna gain.
Power density from radar, 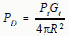 [1]
[1]
If you could cover the entire spherical segment with your receiving antenna you would theoretically capture all of the transmitted energy.
You can't do this because no antenna is large enough. (A two degree segment would be about a mile and three-quarters across at fifty miles from
the transmitter.) A receiving antenna captures a portion of this power determined by it's effective capture Area (Ae). The
received power available at the antenna terminals is the power density times the effective capture area (Ae) of the receiving antenna.
For a given receiver antenna size the capture area is constant no matter how far it is from the transmitter, as illustrated in Figure 1.
This concept is shown in the following equation:
 which
is known as the one-way (beacon) equation [2] which
is known as the one-way (beacon) equation [2]
In order to maximize energy transfer between an antenna and transmitter or receiver, the antenna size should correlate λ/4. Control
of beamwidth shape may become a problem when the size of the active element exceeds several wavelengths.
 The relation
between an antenna's effective capture area (Ae) is: The relation
between an antenna's effective capture area (Ae) is:
Antenna Gain, 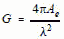 [3]
[3]
or: Equivalent Area, Ae = 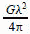 [4]
[4]
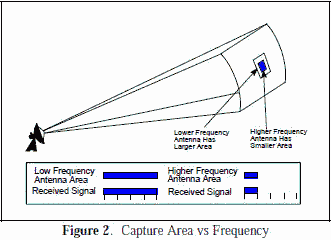
effective aperture is in units of length squared, s proportional to wavelength. This physically means that to maintain the gain when
doubling the frequency, the area is reduced by 1/4. This concept is illustrated in Figure 2. If equation [4] is substituted into equation
[2], the following relationship results: Peak Power at Receiver Input = S (or PR)
= 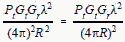 [5] [5]
is the signal calculated one-way from a transmitter to a receiver. For instance, a radar application might be to determine the signal
received by a RWR, ESM, or an ELINT receiver. It is a general purpose equation and could be The free space travel of radio waves can, of course,
be blocked, reflected, or distorted by objects in their path such  As received signal power decreases by 1/4 (6 dB). This is due to the R2
term in equation [5]. It illustrates a square on radius is decreased by 1/2, you further blow up the balloon, so the diameter or radius is doubled,
the square has quadrupled in area. As received signal power decreases by 1/4 (6 dB). This is due to the R2
term in equation [5]. It illustrates a square on radius is decreased by 1/2, you further blow up the balloon, so the diameter or radius is doubled,
the square has quadrupled in area.
The one-way free space loss factor (α1), (sometimes
called the path loss factor) is given by the term 4πR2)(4π/λ2)
or (4πR /λ)2. As shown in Figure 3, the loss is due to the ratio of two factors (1) the effective radiated area
of the transmit antenna, which is the surface area of a sphere (4πR2) at that distance (R), and (2) the
effective capture  area (Ae) of the receive antenna which has a gain of one. If a receiving antenna could capture
the whole surface area of the sphere, there would be no spreading loss, but a practical antenna will capture only a small part of the spherical
radiation. Space loss is calculated using isotropic antennas for both transmit and receive, so α1 is
independent of the actual antenna. Using Gr = 1 in equation [11] in section 3-1, Ae = λ/4π.
Since this term is in the denominator of α1, the higher the frequency (lower λ) the more the space loss.
Since Gt and Gr are part of the one-way radar equation, S (or Pr) is adjusted according to actual antennas
as shown in the last portion of Figure 3. The value of the received signal (S) is: area (Ae) of the receive antenna which has a gain of one. If a receiving antenna could capture
the whole surface area of the sphere, there would be no spreading loss, but a practical antenna will capture only a small part of the spherical
radiation. Space loss is calculated using isotropic antennas for both transmit and receive, so α1 is
independent of the actual antenna. Using Gr = 1 in equation [11] in section 3-1, Ae = λ/4π.
Since this term is in the denominator of α1, the higher the frequency (lower λ) the more the space loss.
Since Gt and Gr are part of the one-way radar equation, S (or Pr) is adjusted according to actual antennas
as shown in the last portion of Figure 3. The value of the received signal (S) is: 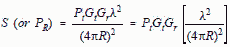 [6] [6]
To convert this equation to dB form, it is rewritten as:
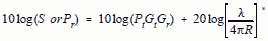 ( keep
λ and R in same units) [7] ( keep
λ and R in same units) [7]
Since λ = c / f, equation [7] can be rewritten as:
10 Log (S or Pr) = 10 Log(PtGtGr) - α1
[8]
Where the one-way free space loss, α1, is defined as:
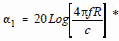 * [9] * [9] The signal received equation in
dB form is: 10log (Pr or S) = 10 log Pt + 10 log Gt + 10 log Gr - α1
[10] The one-way free space loss, α1, can be given in terms of a variable and constant term as
follows:
 [11]
[11]
The value of f1 can be either in MHz or GHz as shown with commonly used units of R in the adjoining table.

Note: To avoid having to include additional terms for these calculations, always combine any transmission line loss with antenna gain.
A value for the one-way free space loss (α1) can be obtained from: (a) The One-way
Free Space Loss graph (Figure 4). Added accuracy can be obtained using the Frequency Extrapolation
graph (Figure 5) (b) The space loss nomograph (Figure 6 or 7) (c) The formula for
α1, equation [11]. FOR EXAMPLE: Find the value of the one-way free
space loss, α1, for an RF of 7.5 GHz at 100 NM. (a) From Figure 4, find
100 NM on the X-axis and estimate where 7.5 GHz is located between the 1 and 10 GHz lines
(note dot). Read α1 as 155 dB. An alternate way would be to read the α1
at 1 GHz (138 dB) and add the frequency extrapolation value (17.5 dB for 7.5:1, dot on Figure
5) to obtain the same 155 dB value. (b) From the nomogram
(Figure 6), the value of α1 can be read as 155 dB (Note the dashed line).
(c) From the equation 11, the precise value of α1 is 155.3 dB. Remember,
α1 is a free space value. If there is atmospheric attenuation because of absorption of RF due to certain molecules in the
atmosphere or weather conditions etc., the atmospheric attenuation is in addition to the space loss (refer to Section 5-1).
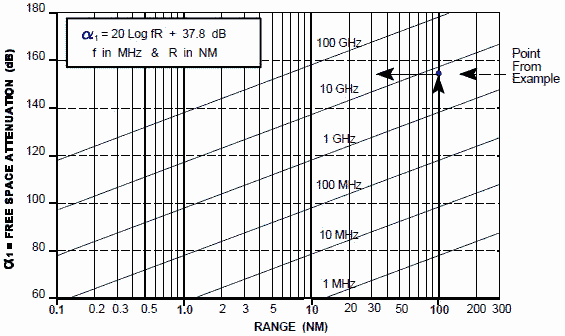
Figure 4. One-Way Free Space Loss
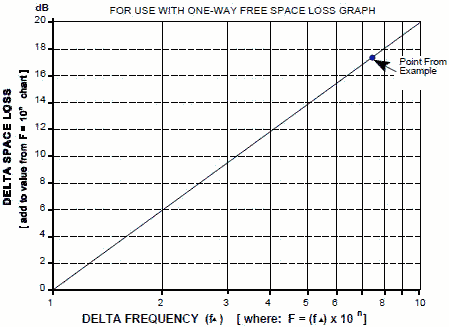
Figure 5. Frequency Extrapolation
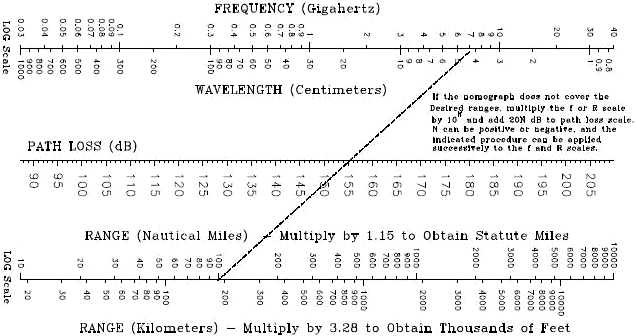
Figure 6. One-Way Space Loss Nomograph For Distances Greater Than 10 Nautical
Miles

Figure 7. One-Way Space Loss Nomograph For Distances Less Than 10 Nautical
Miles
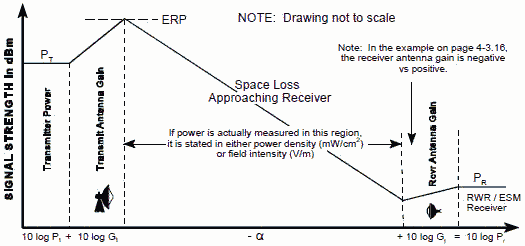
Figure 8. Visualization of One-Way Radar Equation RWR/ESM RANGE EQUATION (One-Way) The one-way radar (signal strength) equation [5] is rearranged
to calculate the maximum range Rmax of RWR/ESM receivers. It occurs when the received radar signal just equals Smin as
follows:
 [12]
[12]
In log form: 20 log Rmax = 10 log Pt + 10 log Gt - 10 log Smin - 20 log
f + 20 log(c/4π) [13]
and since K1 = 20 log{4π/c times conversion units if not in m/sec, m, and Hz} (Refer to section
4-3 for values of K1). 10 log Rmax = ½[10 log Pt + 10 log Gt - 10 log Smin - 20 log f
- K1] ( keep Pt and Smin in same units) [14]
If you want to convert back from dB, then Rmax � , where M dB is the resulting number in the brackets of equation 14. From Section
5-2, Receiver Sensitivity / Noise, Smin is related to the noise factor S: Smin = (S/N)min
(NF)KToB [15] The
one-way RWR/ESM range equation becomes:
 [16] [16]
RWR/ESM RANGE INCREASE AS A RESULT OF A SENSITIVITY INCREASE
As shown in equation [12] Smin-1 proportional to Rmax. Therefore, -10 log Smin proportional
to 20 log Rmax and the table below results: % Range Increase: Range + (% Range Increase) x Range
= New Range i.e., for a 6 dB sensitivity increase, 500 miles +100% x 500 miles = 1,000 miles Range Multiplier:
Range x Range Multiplier = New Range i.e., for a 6 dB sensitivity increase 500 miles x 2 = 1,000 miles

RWR/ESM RANGE DECREASE AS A RESULT OF A SENSITIVITY DECREASE As shown in equation [12] Smin
proportional to Rmax. Therefore, -10 log Smin proportional to 20 log Rmax and the table below results:
% Range Decrease: Range - (% Range decrease) x Range = New Range i.e., for a 6 dB sensitivity decrease,
500 miles - 50% x 500 miles = 250 miles Range Multiplier: Range x Range Multiplier = New Range i.e., for
a 6 dB sensitivity decrease 500 miles x .5 = 250 miles

Example of One-Way Signal Strength: A 5 (or 7) GHz radar has a 70 dBm signal fed through a 5 dB loss
transmission line to an antenna that has 45 dB gain. An aircraft that is flying 31 km from the radar has an aft EW antenna with -1 dB gain and
a 5 dB line loss to the EW receiver (assume all antenna polarizations are the same). Note: The respective transmission line losses will
be combined with antenna gains, i.e.:
-5 +45 = 40 dB, -5 - 1 = -6 dB, -10 + 5 = -5 dB.
(1) What is the power level at the input of the EW receiver? Answer (1): Pr at the input to the EW receiver = Transmitter
power - xmt cable loss + xmt antenna gain - space loss + rcvr antenna gain - rcvr cable loss. Space loss (from section 4-3) @ 5 GHz =
20 log f R + K1 = 20 log (5x31) + 92.44 = 136.25 dB. Therefore, Pr = 70 + 40 - 136.25 - 6 = -32.25 dBm @ 5 GHz (Pr
= -35.17 dBm @ 7 GHz since α1 = 139.17 dB) (2) If the received signal is fed to a jammer with a gain
of 60 dB, feeding a 10 dB loss transmission line which is connected to an antenna with 5 dB gain, what is the power level from the jammer at
the input to the receiver of the 5 (or 7) GHz radar? Answer (2): Pr at the input to the radar receiver = Power at the input
to the EW receiver+ Jammer gain - jammer cable loss + jammer antenna gain - space loss + radar rcvr antenna gain - radar rcvr cable loss .
Therefore, Pr = -32.25 + 60 - 5 - 136.25 + 40 = -73.5 dBm @ 5 GHz. (Pr = -79.34 dBm @ 7 GHz since
α1 = 139.17 dB and Pt = -35.17 dBm). This problem continues in section 4-4, 4-7, and 4-10.
Table of Contents for Electronics Warfare and Radar Engineering Handbook
Introduction |
Abbreviations | Decibel | Duty
Cycle | Doppler Shift | Radar Horizon / Line
of Sight | Propagation Time / Resolution | Modulation
| Transforms / Wavelets | Antenna Introduction
/ Basics | Polarization | Radiation Patterns |
Frequency / Phase Effects of Antennas |
Antenna Near Field | Radiation Hazards |
Power Density | One-Way Radar Equation / RF Propagation
| Two-Way Radar Equation (Monostatic) |
Alternate Two-Way Radar Equation |
Two-Way Radar Equation (Bistatic) |
Jamming to Signal (J/S) Ratio - Constant Power [Saturated] Jamming
| Support Jamming | Radar Cross Section (RCS) |
Emission Control (EMCON) | RF Atmospheric
Absorption / Ducting | Receiver Sensitivity / Noise |
Receiver Types and Characteristics |
General Radar Display Types |
IFF - Identification - Friend or Foe | Receiver
Tests | Signal Sorting Methods and Direction Finding |
Voltage Standing Wave Ratio (VSWR) / Reflection Coefficient / Return
Loss / Mismatch Loss | Microwave Coaxial Connectors |
Power Dividers/Combiner and Directional Couplers |
Attenuators / Filters / DC Blocks |
Terminations / Dummy Loads | Circulators
and Diplexers | Mixers and Frequency Discriminators |
Detectors | Microwave Measurements |
Microwave Waveguides and Coaxial Cable |
Electro-Optics | Laser Safety |
Mach Number and Airspeed vs. Altitude Mach Number |
EMP/ Aircraft Dimensions | Data Busses | RS-232 Interface
| RS-422 Balanced Voltage Interface | RS-485 Interface |
IEEE-488 Interface Bus (HP-IB/GP-IB) | MIL-STD-1553 &
1773 Data Bus | This HTML version may be printed but not reproduced on websites.
Related Pages on RF Cafe
-
Introduction to Radar (Air University)
- Radar Equation, 2-Way
(another)
-
Radar Equation, 1-Way
-
Radar Equation, Bistatic
-
Radar Techniques - Primer (1945 QST)
- Radar
Postage Stamps
- RF Cafe Quiz #7 - Radar Principles
- AN/MPN-14 USAF Radar Shop
- AN/TPN-19 USAF Radar Shop
- EW/Radar
Handbook - Doppler Shift
- Doppler Shift Calculator
-
Identification Friend or Foe (IFF)
-
Radar Horizon / Line of Sight
- Radar Systems Vendors
-
NEETS Radar Principles
- Radar System Vendors
- Who Invented Radar?
-
Simple Modification Increases ATC Reliability
|









 Recall
from Section 4-2 that the power density at a distant point from a radar with an antenna gain of Gt is the power density from an isotropic
antenna multiplied by the radar antenna gain.
Recall
from Section 4-2 that the power density at a distant point from a radar with an antenna gain of Gt is the power density from an isotropic
antenna multiplied by the radar antenna gain.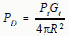 [1]
[1] which
is known as the one-way (beacon) equation [2]
which
is known as the one-way (beacon) equation [2] The relation
between an antenna's effective capture area (Ae) is:
The relation
between an antenna's effective capture area (Ae) is: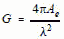 [3]
[3]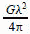 [4]
[4]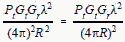 [5]
[5] As received signal power decreases by 1/4 (6 dB). This is due to the R2
term in equation [5]. It illustrates a square on radius is decreased by 1/2, you further blow up the balloon, so the diameter or radius is doubled,
the square has quadrupled in area.
As received signal power decreases by 1/4 (6 dB). This is due to the R2
term in equation [5]. It illustrates a square on radius is decreased by 1/2, you further blow up the balloon, so the diameter or radius is doubled,
the square has quadrupled in area. area (Ae) of the receive antenna which has a gain of one. If a receiving antenna could capture
the whole surface area of the sphere, there would be no spreading loss, but a practical antenna will capture only a small part of the spherical
radiation. Space loss is calculated using isotropic antennas for both transmit and receive, so
area (Ae) of the receive antenna which has a gain of one. If a receiving antenna could capture
the whole surface area of the sphere, there would be no spreading loss, but a practical antenna will capture only a small part of the spherical
radiation. Space loss is calculated using isotropic antennas for both transmit and receive, so 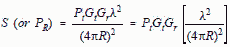 [6]
[6]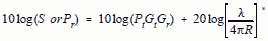 ( keep
λ and R in same units) [7]
( keep
λ and R in same units) [7]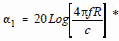 * [9]
* [9] [11]
[11]





 [12]
[12] [16]
[16]

