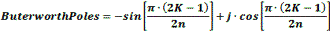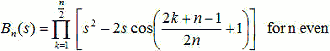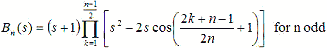|
Butterworth poles lie along a circle and are spaced at equal angular distances
around a circle. It is designed to have a frequency response which is as flat as
mathematically possible in the passband, and is often referred to as a 'maximally
flat magnitude' filter. Prototype value real and imaginary pole locations (ω=1 at
the 3 dB cutoff point) for Butterworth filters are presented in the table below.
The Butterworth type filter was first described by the British engineer Stephen
Butterworth in his paper "On the Theory of Filter Amplifiers", Wireless Engineer
(also called Experimental Wireless and the Wireless Engineer), vol. 7, 1930, pp.
536-541.
See my online filter calculators and plotters
here.
Butterworth filter prototype element values are
here.
Pole locations are calculated as follows, where K=1,2,...,n. n is
the filter order.
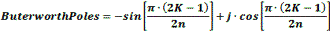
The Butterworth polynomials may be written in complex form as above, but are
usually written with real coefficients by multiplying pole pairs which are complex
conjugates, such as s1 and sn. The polynomials are normalized
by setting ωc = 1.
The normalized Butterworth polynomial equations have the general form:
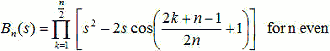
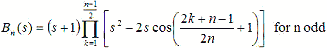
| 1 |
(s + 1) |
| 2 |
(s2 + 1.4142s + 1) |
| 3 |
(s + 1)(s2 + s + 1) |
| 4 |
(s2 + 0.7654s + 1)(s2 + 1.8478s + 1) |
| 5 |
(s + 1)(s2 + 0.6180s + 1)(s2 + 1.6180s + 1) |
| 6 |
(s2 + 0.5176s + 1)(s2 + 1.4142s + 1)(s2 + 1.9319s
+ 1) |
| 7 |
(s + 1)(s2 + 0.4450s + 1)(s2 + 1.2470s
+ 1)(s2 + 1.8019s + 1) |
| 8 |
(s2 + 0.3902s + 1)(s2 + 1.1111s + 1)(s2 + 1.6629s
+ 1)(s2 + 1.9616s + 1) |
| 1 |
1.0000 |
|
| 2 |
0.7071 |
0.7071 |
| 3 |
0.5000 1.0000
|
0.8660 |
| 4 |
0.9239 0.3827
|
0.3827 0.9239
|
| 5 |
0.8090 0.3090
1.0000
|
0.5878 0.9511
|
| 6 |
0.9659 0.7071
0.2588
|
0.2588 0.7071
0.9659
|
| 7 |
0.9010 0.6235
0.2225
1.0000
|
0.4339 0.7818
0.9749
|
| 8 |
0.9808 0.8315
0.5556
0.1951
|
0.1951 0.5556
0.8315
0.9808
|
| 9 |
0.9397 0.7660
0.5000
0.1737
1.0000
|
0.3420 0.6428
0.8660
0.9848
|
| 10 |
0.9877 0.8910
0.7071
0.4540
0.1564
|
0.1564 0.4540
0.7071
0.8910
0.9877
|
 Data taken
from "Filter Design," by Steve Winder, Newnes Press, 1998. This is a great filter
design book, and I recommend you purchase a copy of it.
|
