Butterworth Filter Prototype Element Values | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
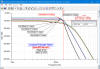
Butterworth poles lie along a circle and are spaced at equal angular distances around a circle. It is designed to have a frequency response which is as flat as mathematically possible in the passband, and is often referred to as a 'maximally flat magnitude' filter. Prototype value real and imaginary pole locations (ω=1 at the 3 dB cutoff point) for Butterworth filters are presented in the table below. The Butterworth type filter was first described by the British engineer Stephen Butterworth in his paper "On the Theory of Filter Amplifiers", Wireless Engineer (also called Experimental Wireless and the Wireless Engineer), vol. 7, 1930, pp. 536-541. The table below lists prototype element values for the normalized lowpass function, which assumes a cutoff frequency of 1 rad/sec and source and load impedances of 1 Ω. Either an input capacitor (top reference line in table) or an input inductor (bottom line in table) can be used. Convert Butterworth prototype values to other cutoff frequencies, impedances, and to highpass, bandpass or bandstop using the equations here. See my online Butterworth filter calculators and plotters here. Complex poles are here.  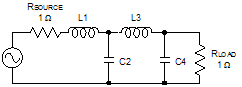Capacitor Input  Inductor Input
Webmaster: Kirt Blattenberger, BSEE, UVM 1989 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
