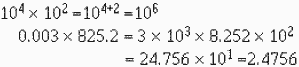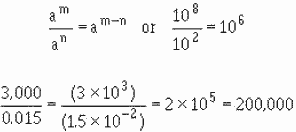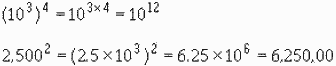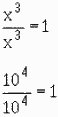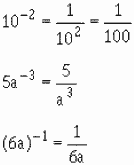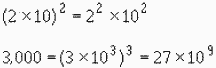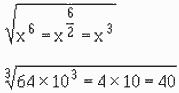RF Cascade Workbook for Excel
RF & Electronics Symbols for Visio
RF & Electronics Symbols for Office
RF & Electronics Stencils for Visio
RF Workbench (shareware)
T-Shirts, Mugs, Cups, Ball Caps, Mouse Pads
Espresso Engineering Workbook™
Smith Chart™ for Excel
|
 |
Module 3 - Introduction to Circuit Protection, Control, and Measurement
Navy
Electricity and Electronics Training Series (NEETS)
Chapter 1: Pages AII-1 through AII-2 |
Module 3 −− Introduction to Circuit Protection, Control, and Measurement
Pages i,
1−1,
1−11,
1−21,
1−31,
1−41,
1−51,
1−61,
1−71,
2−1,
2−11,
1−21,
2−31,
2−41,
3−1,
3−11,
3−21,
3−31,
AI−1,
AII−1,
AIII−1,
IV−1,
Index
Appendix II
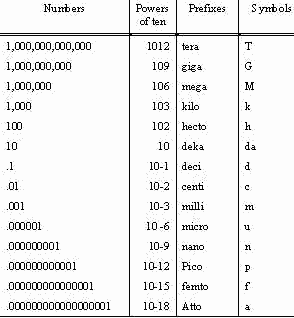
LAWS of EXPONENTS The International Symbols Committee has adopted prefixes for
denoting decimal multiples of units. The National Bureau of Standards has followed the recommendations of this
committee, and has adopted the following list of prefixes:
To multiply like (with same base) exponential quantities, add the exponents. In the language of algebra the
rule is am x an = am+n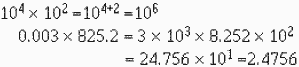 
To divide exponential quantities, subtract the exponents. In the language of algebra the rule is
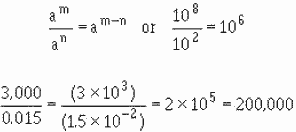
AII-1
To raise an exponential quantity to a power, multiply the exponents. In the language of algebra (xm)n
= xmn.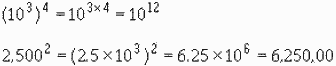 
Any number (except zero) raised to the zero power is one. In the language of algebra x0 = 1
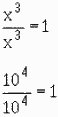
Any base with a negative exponent is equal to 1 divided by the base with an equal positive exponent. In
the language of algebra x-a = 1/xa
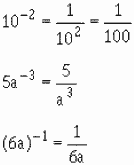
To raise a product to a power, raise each factor of the product to that power.
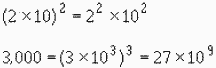
To find the nth root of an exponential quantity, divide the exponent by the index of the root. Thus, the
nth root of am = am.
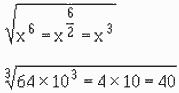
AII-2
| - |
Matter, Energy,
and Direct Current |
| - |
Alternating Current and Transformers |
| - |
Circuit Protection, Control, and Measurement |
| - |
Electrical Conductors, Wiring Techniques,
and Schematic Reading |
| - |
Generators and Motors |
| - |
Electronic Emission, Tubes, and Power Supplies |
| - |
Solid-State Devices and Power Supplies |
| - |
Amplifiers |
| - |
Wave-Generation and Wave-Shaping Circuits |
| - |
Wave Propagation, Transmission Lines, and
Antennas |
| - |
Microwave Principles |
| - |
Modulation Principles |
| - |
Introduction to Number Systems and Logic Circuits |
| - |
- Introduction to Microelectronics |
| - |
Principles of Synchros, Servos, and Gyros |
| - |
Introduction to Test Equipment |
| - |
Radio-Frequency Communications Principles |
| - |
Radar Principles |
| - |
The Technician's Handbook, Master Glossary |
| - |
Test Methods and Practices |
| - |
Introduction to Digital Computers |
| - |
Magnetic Recording |
| - |
Introduction to Fiber Optics |
| Note: Navy Electricity and Electronics Training
Series (NEETS) content is U.S. Navy property in the public domain. |
|
|
Copyright: 1996 - 2024
Webmaster:
Kirt
Blattenberger,
BSEE - KB3UON
RF Cafe began life in 1996 as "RF Tools" in an AOL screen name web space totaling
2 MB. Its primary purpose was to provide me with ready access to commonly needed
formulas and reference material while performing my work as an RF system and circuit
design engineer. The World Wide Web (Internet) was largely an unknown entity at
the time and bandwidth was a scarce commodity. Dial-up modems blazed along at 14.4 kbps
while tying up your telephone line, and a nice lady's voice announced "You've Got
Mail" when a new message arrived...
|
All trademarks, copyrights, patents, and other rights of ownership to images
and text used on the RF Cafe website are hereby acknowledged.
|
|
All trademarks, copyrights, patents, and other rights of ownership to images
and text used on the RF Cafe website are hereby acknowledged.
My Hobby Website:
AirplanesAndRockets.com
|
|
|
 |
