Navy Electricity and Electronics Training Series (NEETS)
Module 10 - Introduction to Wave Propagation, Transmission Lines,

and Antennas
Chapter 3:  Pages 3-41 through 3-50

Figure 3-32. - Voltage, current, and impedance on open line.

At all odd quarter-wave points (1/4λ, 3/4λ, etc.), the voltage is minimum, the current is maximum, and the impedance is minimum. Thus, at all odd quarter-wave points, the open-ended transmission line acts as a series-resonant circuit. The impedance is equivalent to a very low resistance, prevented from being zero only by small circuit losses.

At all even quarter-wave points (1/2λ, 1λ, 3/2λ, etc.), the voltages is maximum, the current is minimum, and the impedance is maximum. Comparison of the line with an LC resonant circuit shows that at an even number of quarter-wavelengths, an open line acts as a parallel-resonant circuit. The impedance is therefore an extremely high resistance.

In addition, resonant open lines may also act as nearly pure capacitances or inductances. The illustration shows that an open line less than a quarter-wavelength long acts as a capacitance. Also, it acts

3-41

as an inductance from 1/4 to 1/2 wavelength, as a capacitance from 1/2 to 3/4 wavelength, and as an inductance from 3/4 to 1 wavelength, etc. a number of open transmission lines, with their equivalent circuits, are shown in the illustration.

Impedance of Various Lengths of Shorted Lines

Follow figure 3-33 as we study the shorted line. At the odd quarter-wavelength points, the voltage is high, the current is low, and the impedance is high. Since these conditions are similar to those found in a parallel-resonant circuit, the shorted transmission line acts as a parallel-resonant circuit at these lengths.

Figure 3-33. - Voltage, current, and impedance on shorted line.

3-42

At the even quarter-wave points voltage is minimum, current is maximum, and impedance is minimum. Since these characteristics are similar to those of a series-resonant LC circuit, a shorted transmission line whose length is an even number of quarter-wavelengths acts as a series-resonant circuit.

Resonant shorted lines, like open-end lines, also may act as pure capacitances or inductances. The illustration shows that a shorted line less than 1/4 wavelength long acts as an inductance. a shorted line with a length of from 1/4 to 1/2 wavelength acts as a capacitance. From 1/2 to 3/4 wavelength, the line acts as an inductance; and from 3/4 to 1 wavelength, it acts as a capacitance, and so on. The equivalent circuits of shorted lines of various lengths are shown in the illustration. Thus, properly chosen line segments may be used as parallel-resonant, series-resonant, inductive, or capacitive circuits.

Standing WAVES ON a Transmission LINE

There is a large variety of terminations for RF lines. Each type of termination has a characteristic effect on the standing waves on the line. From the nature of the standing waves, you can determine the type of termination that produces the waves.

TERMINATION IN Z₀

Termination in Z₀  (characteristic impedance) will cause a constant reading on an ac meter when it is moved along the length of the line. As illustrated in figure 3-34, view A, the curve, provided there are no losses in the line, will be a straight line. If there are losses in the line, the amplitude of the voltage and current will diminish as they move down the line (view B). The losses are due to dc resistance in the line itself.

3-43

 Figure 3-34. - Effects of various terminations on standing waves.

TERMINATION IN an OPEN Circuit

In an open-circuited RF line (figure 3-34, view C), the voltage is maximum at the end, but the current is minimum. The distance between two adjacent zero current points is 1/2λ, and the distance between alternate zero current points is 1. The voltage is zero at a distance of 1/4λ from the end of the line. This is true at any frequency. a voltage peak occurs at the end of the line, at 1/2λ from the end, and at each 1/2λ thereafter.

3-44

TERMINATION IN a Short Circuit

On the line terminated in a short circuit, shown in figure 3-34, view D, the voltage is zero at the end and maximum at 1/4λ from the end. The current is maximum at the end, zero at 1/4λ from the end, and alternately maximum and zero every 1/4λ thereafter.

TERMINATION IN Capacitance

When a line is terminated in capacitance, the capacitor does not absorb energy, but returns all of the energy to the circuit. This means there is 100 percent reflection. The current and voltage relationships are somewhat more involved than in previous types of termination. For this explanation, assume that the capacitive reactance is equal to the Z₀ of the line. Current and voltage are in phase when they arrive at the end of the line, but in flowing through the capacitor and the characteristic impedance (Z₀) connected in series, they shift in phase relationship. Current and voltage arrive in phase and leave out of phase. This results in the standing-wave configuration shown in figure 3-34, view E. The standing wave of voltage is minimum at a distance of exactly 1/8 from the end. If the capacitive reactance is greater than Z₀ (smaller capacitance), the termination looks more like an open circuit; the voltage minimum moves away from the end. If the capacitive reactance is smaller than Z₀, the minimum moves toward the end.

TERMINATION IN Inductance

When the line is terminated in an inductance, both the current and voltage shift in phase as they arrive at the end of the line. When X_L is equal to Z₀, the resulting standing waves are as shown in figure 3-34, view F. The current minimum is located 1/8λ from the end of the line. When the inductive reactance is increased, the standing waves appear closer to the end. When the inductive reactance is decreased, the standing waves move away from the end of the line.

TERMINATION IN a Resistance NOT EQUAL to The Characteristic Impedance (Z₀)

Whenever the termination is not equal to Z₀, reflections occur on the line. For example, if the terminating element contains resistance, it absorbs some energy, but if the resistive element does not equal the Z₀ of the line, some of the energy is reflected. The amount of voltage reflected may be found by using the equation:

Where:

ER  = the reflected voltage

Ei  = the incident voltage

RR  = the terminating resistance

Z₀= the characteristic impedance of the line

If you try different values of R_L in the preceding equation, you will find that the reflected voltage is equal to the incident voltage only when R_L equals 0 or is infinitely large. When R_L equals Z₀, no reflected voltage occurs. When RL is greater than Z₀, E_R  is positive, but less than E_i. As R_L increases and

3-45

approaches an infinite value, E_R  increases and approaches E_i  in value. When R_L is smaller than Z₀, E_R  has a negative value. This means that the reflected voltage is of opposite polarity to the incident wave at the termination of the line. As R_L approaches zero, E_R  approaches E_i  in value. The smaller the value of E_R, the smaller is the peak amplitude of the standing waves and the higher are the minimum values.

TERMINATION IN a Resistance GREATER THAN Z₀

When RL is greater than Z0, the end of the line is somewhat like an open circuit; that is, standing waves appear on the line. The voltage maximum appears at the end of the line and also at half-wave intervals back from the end. The current is minimum (not zero) at the end of the line and maximum at the odd quarter-wave points. Since part of the power in the incident wave is consumed by the load resistance, the minimum voltage and current are less than for the standing waves on an open-ended line. Figure 3-34, view G, illustrates the standing waves for this condition.

TERMINATION IN a Resistance LESS THAN Z₀

When R_L is less than Z₀, the termination appears as a short circuit. The standing waves are shown in figure 3-34, view H. Notice that the line terminates in a current Loop (peak) and a voltage NODE (minimum). The values of the maximum and minimum voltage and current approach those for a shorted line as the value of R_L approaches zero.

A line does not have to be any particular length to produce standing waves; however, it cannot be an infinite line. Voltage and current must be reflected to produce standing waves. For reflection to occur, a line must not be terminated in its characteristic impedance. Reflection occurs on lines terminated in opens, shorts, capacitances, and inductances, because no energy is absorbed by the load. If the line is terminated in a resistance not equal to the characteristic impedance of the line, some energy will be absorbed and the rest will be reflected.

The voltage and current relationships for open-ended and shorted lines are opposite to each other, as shown in figure 3-34, views C and D. The points of maximum and minimum voltage and current are determined from the output end of the line, because reflection always begins at that end.

Q26.   a nonresonant line is a line that has no standing waves of current and voltage on it and is considered to be flat. Why is this true?

Q27.   On an open line, the voltage and impedance are maximum at what points on the line?

Standing-WAVE RATIO

The measurement of standing waves on a transmission line yields information about equipment operating conditions. Maximum power is absorbed by the load when Z_L = Z₀. If a line has no standing waves, the termination for that line is correct and maximum power transfer takes place.

You have probably noticed that the variation of standing waves shows how near the RF line is to being terminated in Z₀. a wide variation in voltage along the length means a termination far from Z0. a small variation means termination near Z₀. Therefore, the ratio of the maximum to the minimum is a measure of the perfection of the termination of a line. This ratio is called the Standing-WAVE RATIO (swr) and is always expressed in whole numbers. For example, a ratio of 1:1 describes a line terminated in its characteristic impedance (Z₀).

3-46

Voltage Standing-Wave Ratio

The ratio of maximum voltage to minimum voltage on a line is called the Voltage Standing- WAVE RATIO (vswr). Therefore:

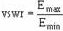
The vertical lines in the formula indicate that the enclosed quantities are absolute and that the two values are taken without regard to polarity. Depending on the nature of the standing waves, the numerical value of vswr ranges from a value of 1 (ZL = Z0, no standing waves) to an infinite value for theoretically complete reflection. Since there is always a small loss on a line, the minimum voltage is never zero and the vswr is always some finite value. However, if the vswr is to be a useful quantity, the power losses along the line must be small in comparison to the transmitted power.

Power Standing-Wave Ratio

The square of the voltage standing-wave ratio is called the Power Standing-WAVE RATIO (pswr). Therefore:

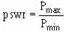
This ratio is useful because the instruments used to detect standing waves react to the square of the voltage. Since power is proportional to the square of the voltage, the ratio of the square of the maximum and minimum voltages is called the power standing-wave ratio. In a sense, the name is misleading because the power along a transmission line does not vary.

Current Standing-Wave Ratio

The ratio of maximum to minimum current along a transmission line is called CURRENT Standing-WAVE RATIO (iswr). Therefore:

This ratio is the same as that for voltages. It can be used where measurements are made with loops that sample the magnetic field along a line. It gives the same results as vswr measurements.

Q28.   At what point on an open-circuited RF line do voltage peaks occur?

Q29.   What is the square of the voltage standing-wave ratio called?

Q30.   What does vswr measure?

3-47

Summary

This chapter has presented information on the characteristics of transmission lines. The information that follows summarizes the important points of this chapter.

Transmission Lines are devices for guiding electrical energy from one point to another.

Input Impedance is the ratio of voltage to current at the input end of a transmission line.

Output Impedance is the ratio of voltage to current at the output end of the line.

TWO-Wire OPEN Lines are parallel lines and have uses such as power lines, rural telephone lines, and telegraph lines. This type of line has high radiation losses and is subject to noise pickup.

TWIN LEAD has parallel lines and is most often used to connect televisions to their antennas.

A TWIsTED PAIR consists of two insulated wires twisted together. This line has high insulation loss.

3-48

A SHIELDED PAIR has parallel conductors separated by a solid dielectric and surrounded by copper braided tubing. The conductors are balanced to ground.

RIGID COAXIAL LINE contains two concentric conductors insulated from each other by spacers. Some rigid coaxial lines are pressurized with an inert gas to prevent moisture from entering. High-frequency losses are less than with other lines.

FLEXIBLE COAXIAL Lines consist of a flexible inner conductor and a concentric outer conductor of metal braid. The two are separated by a continuous insulating material.

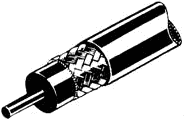WAVEGUIDES are hollow metal tubes used to transfer energy from one point to another. The energy travels slower in a waveguide than in free space.

3-49

COPPER LOSSES can result from power  (I² R) loss, in the form of heat, or skin effect. These losses decrease the conductivity of a line.

Dielectric LOSSES are caused by the heating of the dielectric material between conductors, taking power from the source.

Radiation and INDUCTION LOSSES are caused by part of the electromagnetic fields of a conductor being dissipated into space or nearby objects.

A transmission line is either electrically Long or Short if its physical length is not equal to 1/4λ for the frequency it is to carry.

LUMPED CONSTANTS are theoretical properties (inductance, resistance, and capacitance) of a transmission line that are lumped into a single component.

Distributed CONSTANTS are constants of inductance, capacitance and resistance that are distributed along the transmission line.

3-50