Module 10 - Introduction to Wave Propagation, Transmission Lines, and Antennas

Navy Electricity and Electronics Training Series (NEETS)
Chapter 4:  Pages 4-11 through 4-20

Figure 4-8. - Satellite transmissions using polarized radiation.

Advantages of Vertical Polarization

Simple vertical antennas can be used to provide OMNIDirectIONAL (all directions) communication. This is an advantage when communications must take place from a moving vehicle.

In some overland communications, such as in vehicular installations, antenna heights are limited to 3 meters (10 feet) or less. In such instances vertical polarization results in a stronger receiver signal than does horizontal polarization at frequencies up to about 50 megahertz. From approximately 50 to 100 megahertz, vertical polarization results in a slightly stronger signal than does horizontal polarization with antennas at the same height. Above 100 megahertz, the difference in signal strength is negligible.

For transmission over bodies of water, vertical polarization is much better than horizontal polarization for antennas at the lower heights. As the frequency increases, the minimum antenna height decreases. At 30 megahertz, vertical polarization is better for antenna heights below about 91 meters (300 feet); at 85 megahertz, antenna heights below 15 meters (50 feet); and still lower heights at the high frequencies. Therefore, at ordinary antenna mast heights of 12 meters (40 feet), vertical polarization is advantageous for frequencies less than about 100 megahertz.

Radiation is somewhat less affected by reflections from aircraft flying over the transmission path when vertical polarization is used instead of horizontal polarization. With horizontal polarization, such reflections cause variations in received signal strength. This factor is important in locations where aircraft traffic is heavy.

When vertical polarization is used, less interference is produced or picked up because of strong vhf and uhf broadcast transmissions (television and fm). This is because vhf and uhf transmissions use horizontal polarization. This factor is important when an antenna must be located in an urban area having several television and fm broadcast stations.

4-11

Advantages of Horizontal Polarization

A simple horizontal antenna is bi-directional. This characteristic is useful when you desire to minimize interference from certain directions. Horizontal antennas are less likely to pick up man-made interference, which ordinarily is vertically polarized.

When antennas are located near dense forests or among buildings, horizontally polarized waves suffer lower losses than vertically polarized waves, especially above 100 megahertz. Small changes in antenna locations do not cause large variations in the field intensity of horizontally polarized waves. When vertical polarization is used, a change of only a few meters in the antenna location may have a considerable effect on the received signal strength. This is the result of interference patterns that produce standing waves in space when spurious reflections from trees or buildings occur.

When simple antennas are used, the transmission line, which is usually vertical, is less affected by a horizontally mounted antenna. When the antenna is mounted at right angles to the transmission line and horizontal polarization is used, the line is kept out of the direct field of the antenna. As a result, the radiation pattern and electrical characteristics of the antenna are practically unaffected by the presence of the vertical transmission line.

Q10.   What type of polarization should be used at medium and low frequencies?

Q11.   What is an advantage of using horizontal polarization at high frequencies?

Q12.   What type of polarization should be used if an antenna is mounted on a moving vehicle at frequencies below 50 megahertz?

Radiation Resistance

Radiated energy is the useful part of the transmitter's signal. However, it represents as much of a loss to the antenna as the energy lost in heating the antenna wire. In either case, the dissipated power is equal to I2R. In the case of heat losses, the R is real resistance. In the case of radiation, R is an assumed resistance; if this resistance were actually present, it would dissipate the same amount of power that the antenna takes to radiate the energy. This assumed resistance is referred to as the Radiation Resistance.

Radiation resistance varies at different points on the antenna. This resistance is always measured at a current loop. For the antenna in free space, that is, entirely removed from any objects that might affect its operation, the radiation resistance is 73 ohms. a practical antenna located over a ground plane may have any value of radiation resistance from 0 to approximately 100 ohms. The exact value of radiation resistance depends on the height of the antenna above the ground. For most half-wave wire antennas, the radiation resistance is about 65 ohms. It will usually vary between 55 and 600 ohms for antennas constructed of rod or tubing. The actual value of radiation resistance, so long as it is 50 ohms or more, has little effect on the radiation efficiency of the antenna. This is because the ohmic resistance is about 1 ohm for conductors of large diameter. The ohmic resistance does not become important until the radiation resistance drops to a value less than 10 ohms. This may be the case when several antennas are coupled together.

Radiation TYPES and Patterns

The energy radiated from an antenna forms a field having a definite Radiation Pattern. a radiation pattern is a plot of the radiated energy from an antenna. This energy is measured at various angles at a constant distance from the antenna. The shape of this pattern depends on the type of antenna

4-12

used. In this section, we will introduce the basic types of radiation (isotropic and anisotropic) and their radiation patterns.

Isotropic Radiation

Some antenna sources radiate energy equally in all directions. Radiation of this type is known as Isotropic Radiation. We all know the Sun radiates energy in all directions. The energy radiated from the Sun measured at any fixed distance and from any angle will be approximately the same. Assume that a measuring device is moved around the Sun and stopped at the points indicated in figure 4-9 to make a measurement of the amount of radiation. At any point around the circle, the distance from the measuring device to the Sun is the same. The measured radiation will also be the same. The Sun is therefore considered an isotropic radiator.

Figure 4-9. - Isotropic radiator.

To plot this pattern, we will assume that the radiation is measured on a scale of 0 to 10 units and that the measured amount of radiation is 7 units at all points. We will then plot our measurements on two different types of graphs, rectangular- and polar-coordinate graphs. The RECTANGULAR- COORDINATE GRAPH of the measured radiation, shown in view a of figure 4-10, is a straight line plotted against positions along the circle. View B shows the POLAR-COORDINATE GRAPH for the same isotropic source.

4-13

 Figure 4-10. - Comparison of rectangular- and polar-coordinate graphs for an isotropic source.

In the rectangular-coordinate graph, points are located by projection from a pair of stationary, perpendicular axes. In the polar-coordinate graph, points are located by projection along a rotating axis (radius) to an intersection with one of several concentric, equally-spaced circles. The horizontal axis on the rectangular-coordinate graph corresponds to the circles on the polar-coordinate graph. The vertical axis on the rectangular-coordinate graph corresponds to the rotating axis (radius) on the polar-coordinate graph.

Rectangular-Coordinate Pattern

Look at view a of figure 4-10. The numbered positions around the circle are laid out on the HORIZONTAL AXIs of the graph from 0 to 7 units. The measured radiation is laid out on the VERTICAL AXIs of the graph from 0 to 10 units. The units on both axes are chosen so the pattern occupies a convenient part of the graph.

The horizontal and vertical axes are at a right angle to each other. The point where the axes cross each other is known as the ORIGIN. In this case, the origin is 0 on both axes. Now, assume that a radiation value of 7 units view B is measured at position 2. From position 2 on the horizontal axis, a dotted line is projected upwards that runs parallel to the vertical axis. From position 7 on the vertical axis, a line is projected to the right that runs parallel to the horizontal axis. The point where the two lines cross

(INTERCEPT) represents a value of 7 radiation units at position 2. This is the only point on the graph that can represent this value.

As you can see from the figure, the lines used to plot the point form a rectangle. For this reason, this type of plot is called a rectangular-coordinate graph. a new rectangle is formed for each different point plotted. In this example, the points plotted lie in a straight line extending from 7 units on the vertical scale to the projection of position 7 on the horizontal scale. This is the characteristic pattern in rectangular coordinates of an isotropic source of radiation.

Polar-Coordinate Pattern

The polar-coordinate graph has proved to be of great use in studying radiation patterns. Compare views a and B of figure 4-10. Note the great difference in the shape of the radiation pattern when it is

4-14

transferred from the rectangular-coordinate graph in view a to the polar-coordinate graph in view B. The scale of radiation values used in both graphs is identical, and the measurements taken are both the same. However, the shape of the pattern is drastically different.

Look at view B of figure 4-10 and assume that the center of the concentric circles is the Sun. Assume that a radius is drawn from the Sun (center of the circle) to position 0 of the circle. When you move to position 1, the radius moves to position 1; when you move to position 2, the radius also moves to position 2, and so on.

The positions where a measurement was taken are marked as 0 through 7 on the graph. Note how the position of the radius indicates the actual direction from the source at which the measurement was taken. This is a distinct advantage over the rectangular-coordinate graph in which the position is indicated along a straight-line axis and has no physical relation to the actual direction of measurement. Now that we have a way to indicate the direction of measurement, we must devise a way to indicate the magnitude of the radiation.

Notice that the rotating axis is always drawn from the center of the graph to some position on the edge of the graph. As the axis moves toward the edge of the graph, it passes through a set of equally-spaced, concentric circles. In this example view B, they are numbered successively from 1 to 10 from the center out. These circles are used to indicate the magnitude of the radiation.

The advantages of the polar-coordinate graph are immediately evident. The source, which is at the center of the observation circles, is also at the center of the graph. By looking at a polar-coordinate plot of a radiation pattern, you can immediately see the direction and strength of radiation put out by the source. Therefore, the polar-coordinate graph is more useful than the rectangular-coordinate graph in plotting radiation patterns.

Anisotropic Radiation

Most radiators emit (radiate) stronger radiation in one direction than in another. a radiator such as this is referred to as ANIsotropic. An example of an anisotropic radiator is an ordinary flashlight. The beam of the flashlight lights only a portion of the space surrounding it. If a circle is drawn with the flashlight as the center, as shown in view B of figure 4-11, the radiated light can be measured at different positions around the circle. Again, as with the isotropic radiator, all positions are the same distance from the center, but at different angles. However, in this illustration the radiated light is measured at 16 different positions on the circle.

4-15

Figure 4-11. - Anisotropic radiator.

Directly behind the flashlight (position 0) the radiation measured is minimum. Accordingly, a 0 value is assigned to this position in the rectangular-coordinate graph (fig. 4-11, view A). This radiation remains at minimum until position 4 is reached. Between positions 4 and 6, the measuring device enters the flashlight beam. You can see this transition from darkness to brightness easily in view B. Radiation is fairly constant between positions 6 and 10. Maximum brightness occurs at position 8, which is directly in the path of the flashlight beam. From positions 10 to 12, the measuring device leaves the flashlight beam and the radiation measurement falls off sharply. At position 13 the radiation is again at 0 and stays at this value back to position 0.

Radiation from a light source and radiation from an antenna are both forms of electromagnetic waves. Therefore, the measurement of radiation of an antenna follows the same basic procedure as that just described for the Sun and the flashlight. Before proceeding further with the study of antenna patterns, you should be sure you understand the methods used to graph the measured radiation (magnitude of the radiation). Study the rectangular- and polar-coordinate systems of plotting presented in the following section.

Q13.   What is the radiation resistance of a half-wave antenna in free space?

Q14.   a radiating source that radiates energy stronger in one direction than another is known as what type of radiator?

Q15.   a radiating source that radiates energy equally in all directions is known as what type of radiator?

Q16.   a flashlight is an example of what type of radiator?

In figure 4-11, view A, the radiation pattern of the flashlight is graphed in rectangular coordinates. The illustration of the flashlight beam in view B clearly indicates the shape of the flashlight beam. This is not evident in the radiation pattern plotted on the rectangular-coordinate graph. Now look at figure 4-12. The radiation pattern shown in this figure looks very much like the actual flashlight beam. The pattern in figure 4-12 is plotted using the same values as those of figure 4-11, view A, but is drawn using polar coordinates.

4-16

 Figure 4-12. - Polar-coordinate graph for anisotropic radiator.

The positions marked off on the two polar-coordinate graphs in figures 4-10 and 4-12 were selected and numbered arbitrarily. However, a standard method allows the positions around a source to be marked off so that one radiation pattern can easily be compared with another. This method is based on the fact that a circle has a radius of 360 degrees. The radius extending vertically from the center (position 0 in figure 4-10) is designated 0 degrees. At position 4 the radius is at a right angle to the 0-degree radius. Accordingly, the radius at position 4 is marked 90 degrees, position 8 is 180 degrees, position 12 is 270 degrees, and position 16 is 360 degrees. The various radii drawn on the graph are all marked according to the angle each radius makes with the reference radius at 0 degrees.

The radiation pattern in figure 4-12 is obtained by using the same procedure that was used for (figure 4-10, view B). The radiation measured at positions 1, 2, 3, and 4 is 0. Position 5 measures approximately 1 unit. This is marked on the graph and the rotating radius moves to position 6. At this position a reading of 5.5 units is taken. As before, this point is marked on the graph. The procedure is repeated around the circle and a reading is obtained from positions 6 through 11. At position 12 no radiation is indicated, and this continues on to position 16.

The polar-coordinate graph now shows a definite area enclosed by the radiation pattern. This pattern indicates the general direction of radiation from the source. The enclosed area is called a LOBE. Outside of this area, minimum radiation is emitted in any direction. For example, at position 2 the radiation is 0. Such a point is called a NULL. In real situations, some radiation is usually transmitted in all directions. Therefore, a null is used to indicate directions of minimum radiation. The pattern of figure 4-12 shows one lobe and one continuous null.

Antenna LoadING

You will sometimes want to use one antenna system for transmitting and receiving on several different frequencies. Since the antenna must always be in resonance with the applied frequency, you may need to either physically or electrically lengthen or shorten the antenna.

4-17

Except for trailing-wire antennas used in aircraft installations (which may be lengthened or shortened), physically lengthening the antenna is not very practical. But you can achieve the same result by changing the electrical length of the antenna. To change the electrical length, you can insert either an inductor or a capacitor in series with the antenna. This is shown in figure 4-13, views a and B. Changing the electrical length by this method is known as LUMPED-Impedance TUNING, or LoadING. The electrical length of any antenna wire can be increased or decreased by loading. If the antenna is too short for the wavelength being used, it is resonant at a higher frequency than that at which it is being excited. Therefore, it offers a capacitive reactance at the excitation frequency. This capacitive reactance can be compensated for by introducing a lumped-inductive reactance, as shown in view A. Similarly, if the antenna is too long for the transmitting frequency, it offers an inductive reactance. Inductive reactance can be compensated for by introducing a lumped-capacitive reactance, as shown in view B. An antenna without loading is represented in view C.

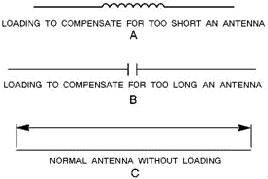
Figure 4-13. - Electrically equal antenna.

Basic Antennas

Before you look at the various types of antennas, consider the relationship between the wavelength at which the antenna is being operated and the actual length of the antenna. An antenna does not necessarily radiate or receive more energy when it is made longer. Specific dimensions must be used for efficient antenna operation.

Nearly all antennas have been developed from two basic types, the Hertz and the Marconi. The basic Hertz antenna is 1/2 wavelength long at the operating frequency and is insulated from ground. It is often called a DIPOLE or a DOUBLET. The basic Marconi antenna is 1/4 wavelength long and is either grounded at one end or connected to a network of wires called a COUNTERPOIsE. The ground or counterpoise provides the equivalent of an additional 1/4 wavelength, which is required for the antenna to resonate.

Half-WAVE Antennas

A half-wave antenna (referred to as a dipole, Hertz, or doublet) consists of two lengths of wire rod, or tubing, each 1/4 wavelength long at a certain frequency. It is the basic unit from which many complex antennas are constructed. The half-wave antenna operates independently of ground; therefore, it may be installed far above the surface of the Earth or other absorbing bodies. For a dipole, the current is

4-18

maximum at the center and minimum at the ends. Voltage is minimum at the center and maximum at the ends, as was shown in figure 4-6.

Radiation Patterns

In the following discussion, the term DIPOLE is used to mean the basic half-wave antenna. The term DOUBLET is used to indicate an antenna that is very short compared with the wavelength of the operating frequency. Physically, it has the same shape as the dipole.

Radiation Pattern of a DOUBLET. - The doublet is the simplest form of a practical antenna. Its radiation pattern can be plotted like the radiation pattern of the flashlight (fig. 4-12). Figure 4-14 shows the development of vertical and horizontal patterns for a doublet. This in NOT a picture of the radiation, but three-dimensional views of the pattern itself. In three views the pattern resembles a doughnut. From the dimensions in these views, two types of polar-coordinate patterns can be drawn, horizontal and vertical. The HORIZONTAL Pattern view a is derived from the solid pattern view C by slicing it horizontally. This produces view B, which is converted to the polar coordinates seen in view A. The horizontal pattern illustrates that the radiation is constant in any direction along the horizontal plane.

Figure 4-14. - Development of vertical and horizontal patterns.

A VERTICAL Pattern view E is obtained from the drawing of the vertical plane view D of the radiation pattern view C. The radiation pattern view C is sliced in half along a vertical plane through the antenna. This produces the vertical plane pattern in view D. Note how the vertical plane in view D of the radiation pattern differs from the horizontal plane in view B. The vertical pattern view E exhibits two lobes and two nulls. The difference between the two patterns is caused by two facts: (1) no radiation is

4-19

emitted from the ends of the doublet; and (2) maximum radiation comes from the doublet in a direction perpendicular to the antenna axis. This type of radiation pattern is both NONDirectIONAL (in a horizontal plane) and DirectIONAL (in a vertical plane).

From a practical viewpoint, the doublet antenna can be mounted either vertically or horizontally. The doublet shown in figure 4-14 is mounted vertically, and the radiated energy spreads out about the antenna in every direction in the horizontal plane. Since ordinarily the horizontal plane is the useful plane, this arrangement is termed NONDirectIONAL. The directional characteristics of the antenna in other planes is ignored. If the doublet were mounted horizontally, it would have the effect of turning the pattern on edge, reversing the patterns given in figure 4-14. The antenna would then be directional in the horizontal plane. The terms "directional" and "nondirectional" are used for convenience in describing specific radiation patterns. a complete description always involves a figure in three dimensions, as in the radiation pattern of figure 4-14.

Q17.   What terms are often used to describe basic half-wave antennas?

Q18.   If a basic half-wave antenna is mounted vertically, what type of radiation pattern will be produced?

Q19.   In which plane will the half-wave antenna be operating if it is mounted horizontally?

Radiation Pattern of a DIPOLE. - The radiation pattern of a dipole (fig. 4-15) is similar to that of the doublet (fig. 4-14). Increasing the length of the doublet to 1/2 wavelength has the effect of flattening out the radiation pattern. The radiation pattern in the horizontal plane of a dipole is a larger circle than that of the doublet. The vertical-radiation pattern lobes are no longer circular. They are flattened out and the radiation intensity is greater.

Figure 4-15. - Radiation pattern of a dipole.

4-20