|
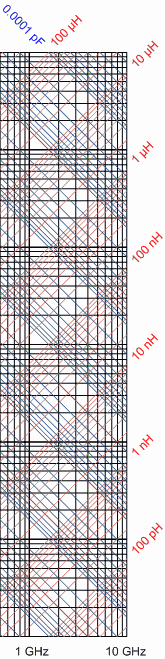 In the
days before a notebook computer on every lab bench, engineers, technicians, scientists, and
hobbyists typically kept charts and nomographs (like this one) all over their office, lab,
and basement walls to be able to quickly determine values without having to whip out the slide
rule or later, a calculator. Sure, calculating the reactance of an inductor or capacitor at
some specific frequency is not rocket science (well, maybe it is to some people), but the
time saved - especially when breadboarding a circuit on the fly - could be significant. Some
of the earlier frequency - reactance nomographs only went up to around 100 kHz (100 kc,
or kilocycles) or even to maybe 10 MHz, because there just was not much design going on then
at such high frequencies. Even today with the low-inductance capacitors and low-capacitance
inductors in surface mount packages, designing above 100 MHz or so can be a black art due
to the stray reactances that generate one or more self-resonance points. The RF Cafe version
goes from 1 Hz to 10 GHz. In the
days before a notebook computer on every lab bench, engineers, technicians, scientists, and
hobbyists typically kept charts and nomographs (like this one) all over their office, lab,
and basement walls to be able to quickly determine values without having to whip out the slide
rule or later, a calculator. Sure, calculating the reactance of an inductor or capacitor at
some specific frequency is not rocket science (well, maybe it is to some people), but the
time saved - especially when breadboarding a circuit on the fly - could be significant. Some
of the earlier frequency - reactance nomographs only went up to around 100 kHz (100 kc,
or kilocycles) or even to maybe 10 MHz, because there just was not much design going on then
at such high frequencies. Even today with the low-inductance capacitors and low-capacitance
inductors in surface mount packages, designing above 100 MHz or so can be a black art due
to the stray reactances that generate one or more self-resonance points. The RF Cafe version
goes from 1 Hz to 10 GHz.
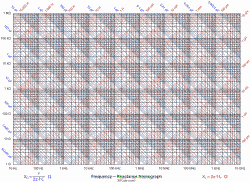 The frequency
- reactance nomograph (chart) below was built on the Visio grid for accuracy, and since it
is in vector format, the size can be increased or decreased without affecting the resolution.
Clicking on the chart will allow you to download the file in GIF format, which can be resized,
but is not truly rescalable. It is 967x706 pixels and prints out nicely as a wall chart. The
image to the right shows a full-size version of the right edge. Why not make the Visio file
available? Right now it has a lot of extra stuff embedded in it that was used to make it accurate,
and the .VSD file is almost 2 MB. It took many hours to create. The frequency
- reactance nomograph (chart) below was built on the Visio grid for accuracy, and since it
is in vector format, the size can be increased or decreased without affecting the resolution.
Clicking on the chart will allow you to download the file in GIF format, which can be resized,
but is not truly rescalable. It is 967x706 pixels and prints out nicely as a wall chart. The
image to the right shows a full-size version of the right edge. Why not make the Visio file
available? Right now it has a lot of extra stuff embedded in it that was used to make it accurate,
and the .VSD file is almost 2 MB. It took many hours to create.
Accuracy of the chart can be easily verified with the standard capacitive reactance and
inductive reactance formulas.
|
XC =
|
1
2π f C
|
XL = 2π f L
|
|
f in Hertz C in Farads L in Henries
|
Example:
What is the inductive reactance of a 1 nH inductor at 1 GHz?
XL = 2π f L = 2π · 109 ·10-9
= 2π = 6.28 Ω
If you look at the small full nomograph, you will see that the bottom axis line is 1 Ω,
and the second up from the bottom is 10 Ω. Follow the angled red 1 nH line to where it
crosses the 1 GHz vertical line. Now, since the bottom line is 1 Ω and the next one up
is 2 Ω. Note that the red line lies between the sixth and seventh lines. On a log scale,
you will recognize that the intersection occurs at around 6.3 Ω - close enough for visual
inspection.
The log-log format for the chart is used traditionally because it allows many decades (cycles)
to be plotted in a relatively small area. If the black primary logarithmic scale was used
on only one axis (either frequency or resistance), the component value lines (capacitor or
inductor) would trace out parabolic curves that would make the log lines for the component
values (blue and red) nearly impossible to draw accurately.
Nomographs / Nomograms Available on RF Cafe:
-
Parallel Series Resistance Calculator -
Transformer Turns Ratio Nomogram -
Symmetrical T and H Attenuator Nomograph -
Amplifier Gain Nomograph -
Decibel
Nomograph -
Voltage and Power Level Nomograph -
Nomograph Construction -
Nomogram Construction for Charts with Complicating Factors or Constants
-
Link Coupling Nomogram -
Multi-Layer Coil Nomograph
-
Delay Line Nomogram -
Voltage, Current, Resistance, and Power Nomograph -
Resistor Selection Nomogram -
Resistance and Capacitance Nomograph -
Capacitance Nomograph -
Earth
Curvature Nomograph -
Coil Winding Nomogram -
RC Time-Constant Nomogram -
Coil Design
Nomograph -
Voltage, Power, and Decibel Nomograph -
Coil Inductance Nomograph -
Antenna Gain Nomograph
-
Resistance and Reactance Nomograph -
Frequency / Reactance Nomograph
|








 In the
days before a notebook computer on every lab bench, engineers, technicians, scientists, and
hobbyists typically kept charts and nomographs (like this one) all over their office, lab,
and basement walls to be able to quickly determine values without having to whip out the slide
rule or later, a calculator. Sure, calculating the reactance of an inductor or capacitor at
some specific frequency is not rocket science (well, maybe it is to some people), but the
time saved - especially when breadboarding a circuit on the fly - could be significant. Some
of the earlier frequency - reactance nomographs only went up to around 100 kHz (100 kc,
or kilocycles) or even to maybe 10 MHz, because there just was not much design going on then
at such high frequencies. Even today with the low-inductance capacitors and low-capacitance
inductors in surface mount packages, designing above 100 MHz or so can be a black art due
to the stray reactances that generate one or more self-resonance points. The RF Cafe version
goes from 1 Hz to 10 GHz.
In the
days before a notebook computer on every lab bench, engineers, technicians, scientists, and
hobbyists typically kept charts and nomographs (like this one) all over their office, lab,
and basement walls to be able to quickly determine values without having to whip out the slide
rule or later, a calculator. Sure, calculating the reactance of an inductor or capacitor at
some specific frequency is not rocket science (well, maybe it is to some people), but the
time saved - especially when breadboarding a circuit on the fly - could be significant. Some
of the earlier frequency - reactance nomographs only went up to around 100 kHz (100 kc,
or kilocycles) or even to maybe 10 MHz, because there just was not much design going on then
at such high frequencies. Even today with the low-inductance capacitors and low-capacitance
inductors in surface mount packages, designing above 100 MHz or so can be a black art due
to the stray reactances that generate one or more self-resonance points. The RF Cafe version
goes from 1 Hz to 10 GHz.
