July 1932 Radio News
 [Table
of Contents] [Table
of Contents]
Wax nostalgic about and learn from the history of early
electronics. See articles from
Radio & Television News, published 1919-1959. All copyrights hereby
acknowledged.
|
I've always disliked book and article
titles containing the word "Modern" because the word is utterly ambiguous and usually
downright misleading more than a few years past the original publication date. What
at publication time was modern is usually obsolete merely a decade later, especially
in the realm of high technology. Sometimes, however, as with this 1932 Radio
News magazine article on insulation (dielectric) breakdown
voltages, bringing the information up to date requires only the addition of an extra
couple decimal points of precision and/or the substitution of a few words. For instance,
replace "condenser" with "capacitor" and units of "mfd" with "μF" and "mmfd"
with "pF." Then you'll be on your way to gaining useful information. You might not
find some of the dielectric types pertinent today, like gutta percha, which is what
covered the world's first transatlantic submerged communications cables. There is
a nice nomograph for use in designing capacitors for specific voltage handling and
a table of dielectric puncturing voltages as well.
Orion Instruments has a very extensive table of
dielectric constant values.
Modern Radio Practice in Using Graphs and Charts - Part 7

Figure 2 - Table of break-down voltages for various types of
sheet insulation (dielectric strength).
By John M. Borst
Part Seven
Calculations in radio design work usually can be reduced to formulas represented
as charts which permit the solution of mathematical problems without mental effort.
This series of articles presents a number of useful charts and explains how others
can be made
The capacity of a homemade condenser is often more or less of a mystery. The
amateur or experimenter who does not possess a bridge or capacity standard must
calculate the capacity. Conversely, if a condenser of a given capacity is desired,
only a calculation will eliminate guesswork.
The standard formula has been transformed into an alignment chart in Figure 1.
The capacity of a condenser can be found when the area of the plates, their number,
distance and the kind of dielectric are known.
The relation between centimeters and inches or mils as well as the relation between
square centimeters and square inches, centimeters and microfarads is also shown
in Figure 1. The "dielectric constant," also called "inductivity" or "specific inductive
capacity," is incorporated on the chart, which makes the consultation of any sources
superfluous.
The formula for the capacity of a condenser consisting of parallel plates is
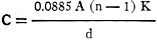 in
micro-microfarads in
micro-microfarads
where A = the area of one plate in square centimeters
d = the distance
between two plates in centimeters
n = the number of
plates
K = the specific
inductive capacity
This expression refers to a condenser with alternate plates in parallel. The
formula does not take into consideration the spreading of the lines of force at
the edges of the plates. This effect is negligible so long as the thickness of the
dielectric is small compared to the area of the plates.
In designing this chart the prime idea has been to cover all possible cases which
occur in practice. Therefore, the capacity scale ranges from 1 micro-microfarad
to over 10 micro-farads, and the other quantities also cover a wide range.
Examples

A Chart (Nomograph) That Works For You
Figure 1 - The size of condenser plates their distance apart,
the number of plates, kind of dielectric or capacity can be found from this chart
if the other four quantities are known. The five quantities are on three straight
lines as shown in the example above.
Two metal plates have an area of 1 square inch and are placed parallel, 1/4 inch
apart, in air. What is the capacity?
Referring to the chart, draw a line from the 1-square-inch mark on the "Area"
scale to 1 on the K scale. The specific inductive capacity of air is one (unity).
This gives you an intersection on the turning scale No. 1. From this newly found
point draw another line through the point 2 on the N scale and find a second point
on the turning scale No.2. The final line is drawn through the latter point and
the 250-mils mark on the d scale. This line intersects the capacity scale at 0.9 mmfd.
When exactly 1 mmfd. is required, the last line should be turned around
its point on the turning scale No. 2 until it intersects the capacity scale at the
1 mmfd. mark and the intersection on the d scale shows the required distance
between the plates (225 mils). The distance, however, can be left the same
and the problem worked backwards, in which case an area of 1.1 square inch is found
necessary. These lines have not been added in Figure 1 because they are so
close together that it might confuse the reader.
When using these charts. needless to say, one should not actually draw the lines
but use a transparent ruler, a regular ruler or a tight thread.
The second example shows how to work the problem backward. Suppose a paper condenser
of 1 mfd. is wanted and the dielectric available has a thickness of 2 mils.
This is manila paper, treated with paraffin. Its specific inductive capacity is
3.65 and the break-down voltage may run as high as 250 volts per mil. There is one
more quantity which can be chosen and then the other one is determined. This can
be either the number of plates or the size of the plates. The number of plates is
the best to assume, because this has to be a whole number. Let us assume there shall
be 30 plates.
For the solution of this problem, start at the 1 mfd. mark on the capacity scale.
A line from this point to the 2 mil. mark on the d scale intersects the turning
scale No. 2. Draw a line through the latter point and through the point representing
the number of plates (30). Now note the intersection on the turning scale No. 1.
Finally draw the last line from the point representing the dielectric constant.
3.65, through the point on the turning scale No.2, which shows the necessary area
of the plates as 84 square inches. As a check-up, an actual calculation gave the
area as 83.7 square inches.
The experience of this second example teaches us that in certain cases the last
line would intersect the area scale beyond the limits of the paper. This means that
the area of the plates needed is going to be larger than 100 square inches. If the
area is to be smaller than 100 square inches, either the number of plates have to
be increased, the thickness of the dielectric decreased or the material exchanged
for one with a greater inductivity. Then try again.
If one wishes the problem solved for values of variables outside the range of
the chart, then some multiplying stunt has to be employed. For instance, suppose
the paper in the above example had been dry paper with a dielectric constant of
1.8, then the last line does not intersect the area scale within the limits of the
page. Therefore, multiplying 1.8 with any convenient number - say, 5 - the last
line is drawn from 9 through the intersection on the turning scale number one and
the area scale is intersected at 34.
This result must now be multiplied by five in order to find the correct answer,
which is 170 square inches.
While determining the specifications for a condenser it is important to be sure
that the dielectric will stand the applied voltage. Therefore a list of the break-down
voltages for different materials is found in Figure 2.
Capacity of a Condenser (aka Capacitor)
Temperature influences the ability of a dielectric to withstand electric pressure.
When the condenser heats up under a continuous load, the breakdown voltage is lowered.
Therefore the tests of such condensers must be made over a considerable time at
working voltage or at a much higher voltage for a short time.
Commercial paper condensers usually consist of long strips of prepared paper,
with tinfoil interleaved, which is then rolled. In the case of rolling a condenser
with an even number of plates, the top plate and the bottom plate form an additional
section of the condenser so that in this case the rolling has the effect of adding
one more plate. The reader should see whether the dielectric for this additional
section has the same thickness as the other sections and make allowances for any
possible difference.
When the number of plates is odd or when the paper is not rolled, the actual
number of plates is used for the calculation.
The accuracy of a calculation by means of this chart will be sufficient only
if the correct values for the dielectric constant and the thickness of the dielectric
have been determined. This is sometimes difficult to accomplish, especially with
paper as a dielectric. If the reader guesses at the constant and the actual separation
of the plates, he must expect the result to be off accordingly.
Nomographs / Nomograms Available on RF Cafe:
-
Parallel Series Resistance Calculator -
Transformer Turns Ratio Nomogram -
Symmetrical T and H Attenuator Nomograph -
Amplifier Gain Nomograph -
Decibel
Nomograph -
Voltage and Power Level Nomograph -
Nomograph Construction -
Nomogram Construction for Charts with Complicating Factors or Constants
-
Link Coupling Nomogram -
Multi-Layer Coil Nomograph
-
Delay Line Nomogram -
Voltage, Current, Resistance, and Power Nomograph -
Resistor Selection Nomogram -
Resistance and Capacitance Nomograph -
Capacitance Nomograph -
Earth
Curvature Nomograph -
Coil Winding Nomogram -
RC Time-Constant Nomogram -
Coil Design
Nomograph -
Voltage, Power, and Decibel Nomograph -
Coil Inductance Nomograph -
Antenna Gain Nomograph
-
Resistance and Reactance Nomograph -
Frequency / Reactance Nomograph
Posted December 29, 2021
(updated from original post on 9/10/2013)
|










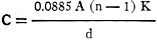 in
micro-microfarads
in
micro-microfarads 
