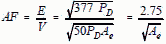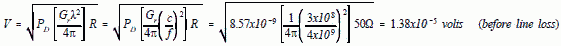|
EMISSION CONTROL (EMCON)
When EMCON is imposed, RF emissions must not exceed -110 dBm/meter2
at one nautical mile. It is best if systems meet EMCON when in either the Standby
or Receive mode versus just the Standby mode (or OFF). If one assumes antenna gain
equals line loss, then emissions measured at the port of a system must not exceed
-34 dBm (i.e. the stated requirement at one nautical mile is converted to a measurement
at the antenna of a point source - see Figure 1). If antenna gain is greater than
line loss (i.e. gain 6 dB, line loss 3 dB), then the -34 dBm value would be lowered
by the difference and would be -37 dBm for the example. The opposite would be true
if antenna gain is less.
 Figure 1. EMCON
Field Intensity / Power Density Measurements
To compute the strength of emissions at the antenna port in Figure 1, we
use the power density equation (see Section 4-2) 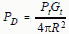 [1] or rearranging
PtGt = PD (4πR2)
[2]
[1] or rearranging
PtGt = PD (4πR2)
[2] Given that PD = -110 dBm/m2 = (10)-11
mW/m2 , and R = 1 NM = 1852 meters. PtGt
= PD(4πR2) = (10 mW/m2)(4π)(1852m)2 = 4.31(10)-4 mW = -33.65
= -34 dBm at the RF system antenna as given. or, the equation can be rewritten
in Log form and each term multiplied by 10: 10log Pt + 10log Gt
= 10log PD + 10log (4πR2)
[3] Since the m2 terms on the right side of equation [3] cancel,
then: 10log Pt + 10log Gt = -110 dBm + 76.35 dB = -33.65
dBm = -34 dBm as given in Figure 1. If MIL-STD-461B/C RE02 (or MIL-STD-461D
RE-102) measurements (see Figure 2) are made onseam/connector leakage of a system,
emissions below 70 dBμV/meter which are measured at one meter will meet the EMCON
requirement. Note that the airframe provides attenuation so portions of systems
mounted inside an aircraft that measure 90 dBμV/meter will still meet EMCON if the
airframe provides 20 dB of shielding (note that the requirement at one nm is converted
to what would be measured at one meter from a point source). The narrowband
emission limit shown in Figure 2 for RE02/RE102 primarily reflect special concern
for local oscillator leakage during EMCON as opposed to switching transients which
would apply more to the broadband limit.
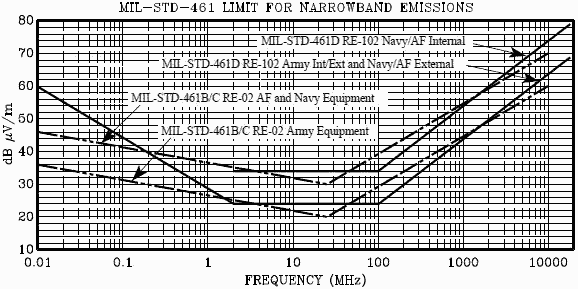 Figure 2. MIL-STD-461
Narrowband Radiated Emissions Limits
Note that in MIL-STD-461D, the narrowband radiated emissions limits were
retitled RE-102 from the previous RE-02 and the upper frequency limit was raised
from 10 GHz to 18 GHz. The majority of this section will continue to reference RE02
since most systems in use today were built to MIL-STD-461B/C. For the other
calculation involving leakage (to obtain 70 dBμV/m) we again start with:
 and use the previous fact that: 10log (PtGt)
= -33.6 dBm = 4.37x10-4 mW (see Section 2-4). The measurement
is at one meter so R2 = 1 m2 we have:  = .348x10-4 mW/m2 = -44.6 dBm/m2 = PD
@ 1 meter
= .348x10-4 mW/m2 = -44.6 dBm/m2 = PD
@ 1 meter Using the field intensity and power density relations (see Section
4-1) 
Changing to microvolts (1V = 106
μV) and converting to logs we have: 20 log (E) = 20 log (106 x
36.2x10-4) = 20 log (.362x104) = 71.18 dBμV/m = 70 dBμV/m
as given in Figure 1. Some words of Caution
A common error is to only use the one-way free space loss coefficient
α1 directly from Figure 6, Section 4-3 to
calculate what the output power would be to achieve the EMCON limits at 1 NM. This
is incorrect since the last term on the right of equation [3] (10 Log(4πR2)) is simply the Log of the surface area of
a sphere - it is NOT the one-way free space loss factor
α1. You cannot interchange power (watts or
dBW) with power density (watts/m2 or dBW/m2). The equation
uses power density (PD), NOT received power (Pr). It is independent
of RF and therefore varies only with range. If the source is a transmitter and/or
antenna, then the power-gain product (or EIRP) is easily measured and it's readily
apparent if 10log (PtGt) is less than -34 dBm. If the output
of the measurement system is connected to a power meter in place of the system transmission
line and antenna, the -34 dBm value must be adjusted. The measurement on the power
meter (dBm) minus line loss (dB) plus antenna gain (dB) must not be higher than
-34 dBm. However, many sources of radiation are through leakage, or are otherwise
inaccessible to direct measurement and PD must be measured with an antenna and a
receiver. The measurements must be made at some RF(s), and received signal strength
is a function of the antenna used therefore measurements must be scaled with an
appropriate correction factor to obtain correct power density.
RE-02 Measurements When RE-02 measurements are
made, several different antennas are chosen dependent upon the frequency range under
consideration. The voltage measured at the output terminals of an antenna is not
the actual field intensity due to actual antenna gain, aperture characteristics,
and loading effects. To account for this difference, the antenna factor is defined
as: AF = E/V
[4] where E = Unknown electric field to be determined in V/m ( or μV/m)
V = Voltage measured at the output terminals of the measuring antenna For
an antenna loaded by a 50 Ω line (receiver), the theoretical antenna factor is developed
as follows:

From Section 4-3 we see that Ae = Grλ2 /4π, and from Section 4-1, E2 = 377 PD
therefore we have:

Reducing this to decibel form we have: 20 log
AF = 20logE - 20logV =  with λ in meters and Gain numeric ratio (not
dB) with λ in meters and Gain numeric ratio (not
dB) This equation is plotted in Figure 3. Since all of the equations
in this section were developed using far field antenna theory, use only the indicated
region.
 Figure 3. Antenna
Factor vs Frequency for Indicated Antenna Gain
In practice the electric field is measured by attaching a field intensity
meter or spectrum analyzer with a narrow bandpass preselector filter to the measuring
antenna, recording the actual reading in volts and applying the antenna factor.
20log E = 20log V + 20log AF
[7] Each of the antennas used for EMI measurements normally has a calibration
sheet for both gain and antenna factor over the frequency range that the antenna
is expected to be used. Typical values are presented in Table 1. Table 1. Typical Antenna Factor Values

The antenna factor can also be developed in terms of the receiving
antenna's effective area. This can be shown as follows: 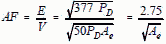
Or in log form: 20logAF =
20logE - 20logV =  While this
relation holds for any antenna, many antennas (spiral, dipole, conical etc.) which
do not have a true "frontal capture area" do not have a linear or logarithmic relation
between area and gain and in that respect the parabolic dish is unique in that the
antenna factor does not vary with frequency, only with effective capture area. Consequently
a larger effective area results in a smaller antenna factor. A calibrated
antenna would be the first choice for making measurements, followed by use of a
parabolic dish or "standard gain" horn. A standard gain horn is one which was designed
such that it closely follows the rules of thumb regarding area/gain and has a constant
antenna factor. If a calibrated antenna, parabolic dish, or "standard horn" is not
available, a good procedure is to utilize a flat spiral antenna (such as the AN/ALR-67
high band antennas). These antennas typically have an average gain of 0 dB (typically
-4 to +4 dB), consequently the antenna factor would not vary a lot and any error
would be small. EXAMPLE: Suppose that
we want to make a very general estimation regarding the ability of a system to meet
EMCON requirements. We choose to use a spiral antenna for measurements and take
one of our samples at 4 GHz. Since we know the gain of the spiral is relatively
flat at 4 GHz and has a gain value of approximately one (0 dB) in that frequency
range. The antenna is connected to a spectrum analyzer by 25 feet of RG9 cable.
We want to take our measurements at 2 meters from the system so our setup is shown
below:

Our RG9 cable has an input impedance of 50Ω, and a loss of 5 dB (from Figure
5, Section 6-1). First, let's assume that we measure -85 dBm at the spectrum
analyzer and we want to translate this into the equivalent strength at 1 NM. Our
power received by the antenna is: Pr = -85 dBm + 5 dB line loss = -80
dBm also PD = Pr/Ae and Ae
= Gλ2/4π = (G/4π)·(c/f)2
= (1/4π)·(3x108/4x109) = 4.47x10-4
m2 in log form: 10 Log PD = 10 Log Pr -
10 Log Ae = -80 dBm + 33.5 = -46.5 dBm/m2 at our 2 meter measuring
point To convert this to a value at 1 NM, we use PtGt
= PD@1 nm 4πR12 = PD@2
m 4πR2 and we solve for PD@1 nm
in log form after cancelling the 4B terms: 10 Log PD@1 nm
= 10 Log PD@2 m + 10 Log (R2m/R1nm) = -46.5 dBm/m2
- 59.3 dB = -105.8 dBm/m2 which is more power than the maximum value
of -110 dBm/m2 specified. If we are making repetitive measurement
as we might do when screening an aircraft on the flight line with numerous systems
installed, or when we want to improve (reduce) the leakage on a single system by
changing antennas, lines, connectors, or EMI gaskets or shielding, this mathematical
approach would be unnecessarily time consuming since it would have to be repeated
after each measurement. A better approach would be to convert the -110 dBm/m2 value
at 1 NM to the maximum you can have at the measuring instrument (in this case a
spectrum analyzer), then you could make multiple measurements and know immediately
how your system(s) are doing. It should be noted that -90 to -100 dBm is about the
minimum signal level that can be detected by a spectrum analyzer, so you couldn't
take measurements much further away unless you used an antenna with a much higher
gain. In order not to exceed EMCON, the power density must not exceed -110
dBm/m2 at 1 NM, which is 10-11 mW/m2.
PtGt = PD@1 nm 4πR12
= PD@2 m 4πR22 and
we solve for PD@1 nm we solve for PD@2 m = 10-11
(1852m)2/(2m)2 = 8.57 x 10 mW/m2 = -50.7 dBm/m2
We'll be using a spectrum analyzer, so we want to compute what the maximum power
or voltage may be. Method 1 - Using the Power Density
Approach Using logs/dB and the values of PD@2 m and Ae
determined previously: 10 Log Pr = 10 Log PD + 10 Log Ae
= -50.7 - 33.5 = -84.2 dBm taking line loss into account we have: -84.2 - 5 dB
= - 89.2 dBm as the maximum measurement reading. If we wanted to calculate
it in volts, and take into account our line impedance we would have the following:
Pr = PDAe = V2/R = V2/50Ω
also Ae = Gλ2/4π so solving for
V we have:
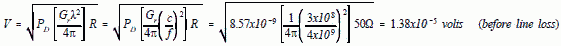
since our line loss is 5 dB, we have -5dB = 20 Log V2/V1.
Solving for V2 we get 7.79x10-6 volts or -89 dBm as a maximum
at our measurement device input. We can see immediately that our value of -85 dBm
that we measured on the previous page would not meet specifications, and neither
would any signal with more power than -89 dBm. Method
2 - Using the Antenna Factor Approach Starting with the same value
of power density that we obtained above (8.57x10-9 W/m2),
we find the field intensity from Table 1, Section 4-1 to be approximately 65 dBμv/m.
Also from Figure 3 in this section, AF = 43 dB @ 4 GHz. (by calculating with equation
[6], the exact value is 42.3 dB) From equation [6]:
20log V = 20log E - 20log AF 20log V = 65 - 43 = 22 dBμv/m. Since
dBμv/m = 20 log (V)(106) = 20 log V + 20 log 106 = 20 log
V + 120 , we see that to get an answer in dBv we must subtract 120 from the dBμv/m
value so: VdB = 22 - 120 = -98 dBv. We then subtract our line loss (-5dB)
and we have: V = -98 - 5 = -103 dBv = 17 dBμv/m = 7.1x10-6 volts
using the fact that P = V2/R and for the input line R = 50Ω, P =
1x10-12 W = -120 dBW = -90 dBm Although this method is just as
accurate as that obtained using method 1, the values obtained in Table 1, Section
4-1, and Figure 3 must be interpolated, and may not result in values which are as
precise as the appropriate formulas would produce. Sample
Problem: What is the approximate transmit power from a receiver? A.
1 nanowatt (nW) F. 100 μW
K. 10 W B. 10 nW
G. 1 milliwatt (mW) L. 100 W C. 100 nW
H. 10 mW
M. 1 kilowatt (kW) D. 1 microwatt (μW) I. 100 mW
N. 10 kW E. 10 μW
J. 1 watt (W)
O. 100 kW The question may seem inappropriate since a receiver is supposedly
a passive device which only receives a signal. If the receiver was a crystal video
receiver as shown in Section 5-3, it wouldn't transmit power unless a built-in-test
(BIT) signal was injected after the antenna to periodically check the integrity
of the microwave path and components. The potential exists for the BIT signal to
leak across switches and couple back through the input path and be transmitted by
the receiver's antennas. If the receiver uses a local oscillator (LO) and
a mixer to translate the signal to an intermediate frequency (IF) for processing
(such as a superhet shown in Section 5-3), there is the potential for the CW LO
signal to couple back through the signal input path and be transmitted by the receiver's
antenna. Normally a mixer has 20 dB of rejection for the reverse direction. In addition,
the LO may be further attenuated by receiver front end filters. In both cases,
the use of isolators described in Section 6-7 could be used to further attenuate
any signals going in the reverse direction, i.e. back to the antenna. A good receiver
design should ensure that any RF leakage radiated by the receiver will not exceed
the EMCON level. In answer to the initial question, "transmit" leakage power
should be less than -34 dBm (0.4 μW) to meet EMCON. Therefore, the real answer may
be "A", "B", or "C" if EMCON is met and could be "D" through possibly "G" if EMCON
is not met.
Table of Contents for Electronics Warfare and Radar Engineering Handbook
Introduction |
Abbreviations | Decibel | Duty
Cycle | Doppler Shift | Radar Horizon / Line
of Sight | Propagation Time / Resolution | Modulation
| Transforms / Wavelets | Antenna Introduction
/ Basics | Polarization | Radiation Patterns |
Frequency / Phase Effects of Antennas |
Antenna Near Field | Radiation Hazards |
Power Density | One-Way Radar Equation / RF Propagation
| Two-Way Radar Equation (Monostatic) |
Alternate Two-Way Radar Equation |
Two-Way Radar Equation (Bistatic) |
Jamming to Signal (J/S) Ratio - Constant Power [Saturated] Jamming
| Support Jamming | Radar Cross Section (RCS) |
Emission Control (EMCON) | RF Atmospheric
Absorption / Ducting | Receiver Sensitivity / Noise |
Receiver Types and Characteristics |
General Radar Display Types |
IFF - Identification - Friend or Foe | Receiver
Tests | Signal Sorting Methods and Direction Finding |
Voltage Standing Wave Ratio (VSWR) / Reflection Coefficient / Return
Loss / Mismatch Loss | Microwave Coaxial Connectors |
Power Dividers/Combiner and Directional Couplers |
Attenuators / Filters / DC Blocks |
Terminations / Dummy Loads | Circulators
and Diplexers | Mixers and Frequency Discriminators |
Detectors | Microwave Measurements |
Microwave Waveguides and Coaxial Cable |
Electro-Optics | Laser Safety |
Mach Number and Airspeed vs. Altitude Mach Number |
EMP/ Aircraft Dimensions | Data Busses | RS-232 Interface
| RS-422 Balanced Voltage Interface | RS-485 Interface |
IEEE-488 Interface Bus (HP-IB/GP-IB) | MIL-STD-1553 &
1773 Data Bus | This HTML version may be printed but not reproduced on websites.
|





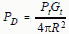 [1] or rearranging
PtGt = PD (4
[1] or rearranging
PtGt = PD (4

 = .348x10-4 mW/m2 = -44.6 dBm/m2 = PD
@ 1 meter
= .348x10-4 mW/m2 = -44.6 dBm/m2 = PD
@ 1 meter


 with λ in meters and Gain numeric ratio (not
dB)
with λ in meters and Gain numeric ratio (not
dB)