|
[Go to TOC]
TWO-WAY RADAR EQUATION (MONOSTATIC)
In this section the radar equation is derived from the one-way equation (transmitter to receiver) which is then extended to the two-way
radar equation. The following is a summary of the important equations to be derived here: Peak power at the radar receiver input
is: 
 Figure 1 illustrates the physical concept and equivalent circuit for a target being illuminated by a monostatic
radar (transmitter and receiver co-located). Note the similarity of Figure 1 to Figure 3 in Section 4-3. Transmitted power, transmitting and
receiving antenna gains, and the one-way free space loss are the same as those described in Section 4-3. The physical arrangement of the elements
is different, of course, but otherwise the only difference is the addition of the equivalent gain of the target RCS factor. Figure 1 illustrates the physical concept and equivalent circuit for a target being illuminated by a monostatic
radar (transmitter and receiver co-located). Note the similarity of Figure 1 to Figure 3 in Section 4-3. Transmitted power, transmitting and
receiving antenna gains, and the one-way free space loss are the same as those described in Section 4-3. The physical arrangement of the elements
is different, of course, but otherwise the only difference is the addition of the equivalent gain of the target RCS factor.
From
Section 4-3, One-Way Radar Equation / RF Propagation, the power in the receiver is:
 [1] [1]
From equation [3] in Section 4-3: Antenna Gain, G =  [2] [2] Similar to a receiving antenna, a radar target
also intercepts a portion of the power, but reflects (reradiates) it in the direction of the radar. The amount of power reflected toward the
radar is determined by the Radar Cross Section (RCS) of the target. RCS is a characteristic of the target that represents its size as seen by
the radar and has the dimensions of area (σ) as shown in Section 4-11. RCS area is not the same as physical area. But, for a radar target, the
power reflected in the radar's direction is equivalent to re-radiation of the power captured by an antenna of area σ (the RCS). Therefore, the
effective capture area (Ae) of the receiving antenna is replaced by the RCS (σ).  [3] so we now have:
[3] so we now have: 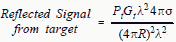 [4] [4]
The equation for the power reflected in the radar's direction is the same as equation [1] except that Pt Gt, which
was the original transmitted power, is replaced with the reflected signal power from the target, from equation [4]. This gives:
 [5]
[5]
 If like
terms are cancelled, the two-way radar equation results. The peak power at the radar receiver input is: If like
terms are cancelled, the two-way radar equation results. The peak power at the radar receiver input is:
 [6]
[6]
* Note: λ=c/f and F = RCS. Keep λ or c, σ, and R in the same units. On reducing equation [6] to log form we have: 10 log Pr = 10 log Pt + 10 log Gt + 10 log Gr + 10 log σ - 20 log
f - 40 log R - 30 log 4π + 20 log c [7]
Target Gain Factor
If Equation [5] terms are rearranged instead of cancelled, a recognizable form results:  [8] [8]
In log form:
 [9]
[9]
The fourth and sixth terms can each be recognized as -α, where α is the one-way
free space loss factor defined in Section 4-3. The fifth term containing RCS (σ) is the only new factor, and it is the "Target Gain Factor".
In simplified terms the equation becomes: 10 log [S (or Pr)] = 10 log Pt + 10 log
Gt + 10 log Gr + Gσ - 2α1 (in dB)
[10]
Where α1 and Gσ are as follows: From Section 4-3, equation [11], the space loss
in dB is given by:  [11] [11]
 * Keep c
and R in the same units. The table of values for K1 is again presented here for completeness. The constant, K1, in the
table includes a range and frequency unit conversion factor. While it's understood that RCS is the antenna aperture area equivalent to an isotropically
radiated target return signal, the target gain factor represents a gain, as shown in the equivalent circuit of Figure 1. The Target Gain Factor
expressed in dB is Gσ as shown in equation [12]. * Keep c
and R in the same units. The table of values for K1 is again presented here for completeness. The constant, K1, in the
table includes a range and frequency unit conversion factor. While it's understood that RCS is the antenna aperture area equivalent to an isotropically
radiated target return signal, the target gain factor represents a gain, as shown in the equivalent circuit of Figure 1. The Target Gain Factor
expressed in dB is Gσ as shown in equation [12].
 [12]
[12]
The "Target Gain Factor" (Gσ) is a composite of RCS, frequency, and dimension conversion factors and is called by various
names: "Gain of RCS", "Equivalent Gain of RCS", "Gain of Target Cross Section", and in dB form "Gain-sub- Sigma". If frequency is given
in MHz and RCS (σ) is in m2, the formula for G is:
 [13]
[13]
or: Gα = 10 log σ + 20 log f1 - 38.54
(in dB) [14]
 For this example,
the constant K2 is -38.54 dB. This value of K2 plus K2 for other area units and frequency multiplier values are summarized in the adjoining
table. For this example,
the constant K2 is -38.54 dB. This value of K2 plus K2 for other area units and frequency multiplier values are summarized in the adjoining
table.
In the two-way radar equation, the one-way free space loss factor (α1) is used twice, once
for the radar transmitter to target path and once for the target to radar receiver path. The radar illustrated in Figure 1 is monostatic so
the two path losses are the same and the values of the two α1's are the same. If the transmission
loss in Figure 1 from Pt to Gt equals the loss from Gr to Pr , and Gr = Gt,
then equation [10] can be written as:
10 log [S or Pr] = 10 log Pt + 20 log Gtr - 2α1
+ Gσ (in dB) [15]
The space loss factor (α1) and the target gain factor (Gσ) include all the necessary unit conversions
so that they can be used directly with the most common units. Because the factors are given in dB form, they are more convenient to use and
allow calculation without a calculator when the factors are read from a chart or nomograph. Most radars are monostatic. That is, the
radar transmitting and receiving antennas are literally the same antenna. There are some radars that are considered "monostatic" but have separate
transmitting and receiving antennas that are colocated. In that case, equation [10] could require two different antenna gain factors as originally
derived:
10 log [S or Pr] = 10 log Pt + 10 log Gt + 10 log Gr - 2α1 + Gσ (in dB) [16]
Note: To avoid having to include additional terms for these calculations, always combine any transmission line loss with antenna gain.
Figure 2 is the visualization of the path losses occurring with the two-way radar equation. Note: to avoid having to include additional
terms, always combine any transmission line loss with antenna gain. Losses due to antenna polarization and atmospheric absorption also need
to be included.

Figure 2. Visualization of Two-Way Radar Equation
RADAR RANGE EQUATION (Two-Way Equation) The Radar Equation is often called the "Radar Range Equation". The
Radar Range Equation is simply the Radar Equation rewritten to solve for maximum Range. The maximum radar range (Rmax) is the distance
beyond which the target can no longer be detected and correctly processed. It occurs when the received echo signal just equals Smin.
The Radar Range Equation is then:  [17] [17]
The first equation, of the three above, is given in Log form by:
 [18]
[18]
As shown previously, Since K1 = 20log [(4B/c) times conversion units if not in m/sec, m, and Hz], we have:
 [19] [19]
 If you want
to convert back from dB, then If you want
to convert back from dB, then 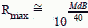
Where M dB is the resulting
number within the brackets of equation 19. From Section 5-2, Receiver Sensitivity / Noise, Smin is related to
the noise factors by:
Smin = (S/N)min(NF)kT0B [20]
The Radar Range Equation for a tracking radar (target continuously in the antenna beam) becomes:
 [21]
[21]
Pt in equations [17], [19], and [21] is the peak power of a CW or pulse signal. For pulse signals these equations assume the radar pulse
is square. If not, there is less power since Pt is actually the average power within the pulse width of the radar signal. Equations [17] and
[19] relate the maximum detection range to Smin, the minimum signal which can be detected and processed (the receiver sensitivity).
The bandwidth (B) in equations [20] and [21] is directly related to Smin. B is approximately equal to 1/PW. Thus a wider pulse width
means a narrower receiver bandwidth which lowers Smin, assuming no integration. One cannot arbitrarily change the receiver
bandwidth, since it has to match the transmitted signal. The "widest pulse width" occurs when the signal approaches a CW signal (see Section
2-11). A CW signal requires a very narrow bandwidth (approximately 100 Hz). Therefore, receiver noise is very low and good sensitivity results
(see Section 5-2). If the radar pulse is narrow, the receiver filter bandwidth must be increased for a match (see Section 5-2), i.e. a 1 μs
pulse requires a bandwidth of approximately 1 MHz. This increases receiver noise and decreases sensitivity. If the radar transmitter
can increase its PRF (decreasing PRI) and its receiver performs integration over time, an increase in PRF can permit the receiver to "pull"
coherent signals out of the noise thus reducing S/Nmin thereby increasing 4-4.6 the detection range. Note that a PRF increase may
limit the maximum range due to the creation of overlapping return echoes (see Section 2-10). There are also other factors that limit
the maximum practical detection range. With a scanning radar, there is loss if the receiver integration time exceeds the radar's time on target.
Many radars would be range limited by line-of-sight/radar horizon (see Section 2-9) well before a typical target faded below Smin.
Range can also be reduced by losses due to antenna polarization and atmospheric absorption (see Sections 3-2 and 5-1).
Two-Way Radar Equation (Example) Assume that a 5 GHz radar has a 70 dBm (10 kilowatt) signal fed through
a 5 dB loss transmission line to a transmit/receive antenna that has 45 dB gain. An aircraft that is flying 31 km from the radar has an RCS
of 9 m2. What is the signal level at the input to the radar receiver? (There is an additional loss due to any antenna polarization
mismatch but that loss will not be addressed in this problem). This problem continues in Sections 4-3, 4-7, and 4-10. Answer:
Starting with: 10 log S = 10 log Pt + 10 log Gt + 10 log Gr + Gσ - 2α1
(in dB) We know that: α1 = 20l og f R + K1 = 20 log (5x31) + 92.44 = 136.25 dB
and that: Gσ = 10 log σ + 20 log f1 + K2 = 10 log 9 + 20 log 5 + 21.46 = 44.98 dB (see Table 1)
(Note: The aircraft transmission line losses (-5 dB) will be combined with the antenna gain (45 dB) for both receive and transmit paths
of the radar) So, substituting in we have: 10 log S = 70 + 40 + 40 + 44.98 - 2(136.25) = -77.52 dBm @ 5 GHz The answer changes
to -80.44 dBm if the tracking radar operates at 7 GHz provided the antenna gains and the aircraft RCS are the same at both frequencies.
α1 = 20 log (7x31) + 92.44 = 139.17 dB, Gσ = 10 log 9 + 20 log 7 + 21.46 = 47.9 dB (see
Table 1) 10 log S = 70 + 40 + 40 + 47.9 - 2(139.17) = -80.44 dBm @ 7 GHz
Table 1. Values of the Target Gain Factor (Gσ) in dB for Various Values of Frequency and RCS

Note: Shaded values were used in the examples. TWO-WAY RADAR RANGE INCREASE AS A RESULT OF A SENSITIVITY
INCREASE As shown in equation [17] Smin-1 ≈ Rmax4 Therefore, -10 log Smin
≈ 40 log Rmax and the table below results: % Range Increase: Range + (% Range Increase) x Range = New Range i.e., for a
12 dB sensitivity increase, 500 miles +100% x 500 miles = 1,000 miles Range Multiplier: Range x Range Multiplier = New Range i.e., for
a 12 dB sensitivity increase 500 miles x 2 = 1,000 miles
Table 2. Effects of Sensitivity Increase 
TWO-WAY RADAR RANGE DECREASE AS A RESULT OF A SENSITIVITY DECREASE As shown in equation
[17] Smin-1 ≈ Rmax4 Therefore, -10 log Smin ≈ 40 log Rmax and the table
below results: % Range Decrease: Range - (% Range Decrease) x Range = New Range i.e., for a 12 dB sensitivity
decrease, 500 miles - 50% x 500 miles = 250 miles Range Multiplier: Range x Range Multiplier = New Range
i.e., for a 12 dB sensitivity decrease 500 miles x 0.5 = 250 miles
Table 3. Effects of Sensitivity Decrease 
Table of Contents for Electronics Warfare and Radar Engineering Handbook
Introduction |
Abbreviations | Decibel | Duty
Cycle | Doppler Shift | Radar Horizon / Line
of Sight | Propagation Time / Resolution | Modulation
| Transforms / Wavelets | Antenna Introduction
/ Basics | Polarization | Radiation Patterns |
Frequency / Phase Effects of Antennas |
Antenna Near Field | Radiation Hazards |
Power Density | One-Way Radar Equation / RF Propagation
| Two-Way Radar Equation (Monostatic) |
Alternate Two-Way Radar Equation |
Two-Way Radar Equation (Bistatic) |
Jamming to Signal (J/S) Ratio - Constant Power [Saturated] Jamming
| Support Jamming | Radar Cross Section (RCS) |
Emission Control (EMCON) | RF Atmospheric
Absorption / Ducting | Receiver Sensitivity / Noise |
Receiver Types and Characteristics |
General Radar Display Types |
IFF - Identification - Friend or Foe | Receiver
Tests | Signal Sorting Methods and Direction Finding |
Voltage Standing Wave Ratio (VSWR) / Reflection Coefficient / Return
Loss / Mismatch Loss | Microwave Coaxial Connectors |
Power Dividers/Combiner and Directional Couplers |
Attenuators / Filters / DC Blocks |
Terminations / Dummy Loads | Circulators
and Diplexers | Mixers and Frequency Discriminators |
Detectors | Microwave Measurements |
Microwave Waveguides and Coaxial Cable |
Electro-Optics | Laser Safety |
Mach Number and Airspeed vs. Altitude Mach Number |
EMP/ Aircraft Dimensions | Data Busses | RS-232 Interface
| RS-422 Balanced Voltage Interface | RS-485 Interface |
IEEE-488 Interface Bus (HP-IB/GP-IB) | MIL-STD-1553 &
1773 Data Bus | This HTML version may be printed but not reproduced on websites.
|



























 Figure 1 illustrates the physical concept and equivalent circuit for a target being illuminated by a monostatic
radar (transmitter and receiver co-located). Note the similarity of Figure 1 to Figure 3 in Section 4-3. Transmitted power, transmitting and
receiving antenna gains, and the one-way free space loss are the same as those described in Section 4-3. The physical arrangement of the elements
is different, of course, but otherwise the only difference is the addition of the equivalent gain of the target RCS factor.
Figure 1 illustrates the physical concept and equivalent circuit for a target being illuminated by a monostatic
radar (transmitter and receiver co-located). Note the similarity of Figure 1 to Figure 3 in Section 4-3. Transmitted power, transmitting and
receiving antenna gains, and the one-way free space loss are the same as those described in Section 4-3. The physical arrangement of the elements
is different, of course, but otherwise the only difference is the addition of the equivalent gain of the target RCS factor. [1]
[1] [2]
[2] [3] so we now have:
[3] so we now have: 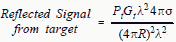 [4]
[4] [5]
[5] If like
terms are cancelled, the two-way radar equation results. The peak power at the radar receiver input is:
If like
terms are cancelled, the two-way radar equation results. The peak power at the radar receiver input is: [6]
[6] [8]
[8] [9]
[9] [11]
[11] * Keep c
and R in the same units. The table of values for K1 is again presented here for completeness. The constant, K1, in the
table includes a range and frequency unit conversion factor. While it's understood that RCS is the antenna aperture area equivalent to an isotropically
radiated target return signal, the target gain factor represents a gain, as shown in the equivalent circuit of Figure 1. The Target Gain Factor
expressed in dB is Gσ as shown in equation [12].
* Keep c
and R in the same units. The table of values for K1 is again presented here for completeness. The constant, K1, in the
table includes a range and frequency unit conversion factor. While it's understood that RCS is the antenna aperture area equivalent to an isotropically
radiated target return signal, the target gain factor represents a gain, as shown in the equivalent circuit of Figure 1. The Target Gain Factor
expressed in dB is Gσ as shown in equation [12]. [12]
[12] [13]
[13] For this example,
the constant K2 is -38.54 dB. This value of K2 plus K2 for other area units and frequency multiplier values are summarized in the adjoining
table.
For this example,
the constant K2 is -38.54 dB. This value of K2 plus K2 for other area units and frequency multiplier values are summarized in the adjoining
table.
 [17]
[17] [18]
[18] [19]
[19] If you want
to convert back from dB, then
If you want
to convert back from dB, then 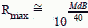
 [21]
[21]


