Electronic Warfare and Radar Systems Engineering Handbook

- Support Jamming -

[Go to TOC]

SUPPORT JAMMING

The following table contains a summary of equations developed in this section:

Support jamming adds a few geometric complexities. A SOJ platform usually uses high gain, directional antennas. Therefore, the jamming antenna must not only be pointed at the victim radar, but there must be alignment of radar, targets, and SOJ platform for the jamming to be effective. Two cases will be described, main lobe-jamming and side-lobe jamming.

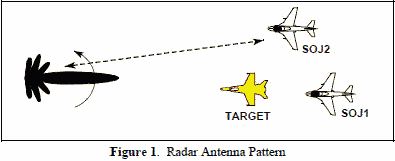
Support jamming is usually applied against search and acquisition radars which continuously scan horizontally through a volume of space. The scan could cover a sector or a full 360°. The horizontal antenna pattern of the radar will exhibit a main lobe and side lobes as illustrated in Figure 1. The target is detected when the main lobe sweeps across it. For main lobe jamming, the SOJ platform and the target(s) must be aligned with the radar's main lobe as it sweeps the target(s).

For side lobe jamming, the SOJ platform may be aligned with one or more of the radar's side lobes when the main lobe sweeps the target. The gain of a radar's side lobes are many tens of dB less (usually more than 30 dB less) than the gain of the main lobe, so calculations of side lobe jamming must use the gain of the side lobe for the radar receive antenna gain, not the gain of the main lobe. Also, because many modern radars employ some form of side lobe blanking or side lobe cancellation, some knowledge of the victim radar is required for the employment of side lobe jamming.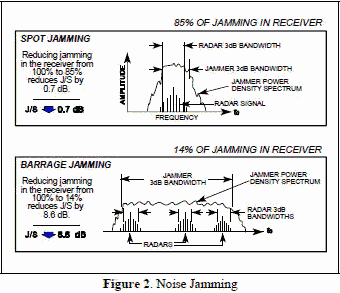

All radar receivers are frequency selective. That is, they are filters that allow only a narrow range of frequencies into the receiver circuitry. DECM, by definition, creates forgeries of the real signal and, ideally, are as well matched to the radar receiver as the real signal. On the other hand, noise jamming probably will not match the radar receiver bandwidth characteristics. Noise jamming is either spot jamming or barrage jamming. As illustrated in Figure 2, spot jamming is simply narrowing the bandwidth of the noise jammer so that as much of the jammer power as possible is in the radar receiver bandwidth. Barrage jamming is using a wide noise bandwidth to cover several radars with one jammer or to compensate for any uncertainty in the radar frequency. In both cases some of the noise power is "wasted" because it is not in the radar receiver filter.

In the past, noise jammers were often described as having so many "watts per MHz". This is nothing more than the power of the noise jammer divided by the noise bandwidth. That is, a 500 watt noise jammer transmitting a noise bandwidth of 200 MHz has 2.5 watts/MHz. Older noise jammers often had noise bandwidths that were difficult, or impossible, to adjust accurately. These noise jammers usually used manual tuning to set the center frequency of the noise to the radar frequency. Modern noise jammers can set on the radar frequency quite accurately and the noise bandwidth is selectable, so the noise bandwidth is more a matter of choice than it used to be, and it is possible that all of the noise is placed in the victim radar's receiver.

If, in the example above, the 500 watt noise jammer were used against a radar that had a 3 MHz receiver bandwidth, the noise jammer power applicable to that radar would be:

3 MHz x 2.5 watts/MHz = 7.5 watts → 38.75 dBm            [1]

The calculation must be done as shown in equation [1] - multiply the watts/MHz by the radar bandwidth first and then convert to dBm. You can't convert to dBm/MHz and then multiply. (See derivation of dB in Section 2-4)

An alternate method for dB calculations is to use the bandwidth reduction factor (BF). The BF is:

                    [2]

where: BW_J is the bandwidth of the noise jammer, and BWR is the bandwidth of the radar receiver.

The power of the jammer in the jamming equation (P_J) can be obtained by either method. If equation [1] is used then P_J is simply 38.75 dBm. If equation [2] is used then the jamming equation is written using (P_J - BF). All the following discussion uses the second method. Which ever method is used, it is required that BW_J ≥ BWR. If BW_J < BW_R, then all the available power is in the radar receiver and equation [1] does not apply and the BF = 0.

MAIN LOBE STAND-OFF / STAND-IN JAMMING

The equivalent circuit shown in Figure 3 applies to main lobe jamming by a stand-off support aircraft or a stand-in RPV. Since the jammer is not on the target aircraft, only two of the three ranges and two of the three space loss factors (α's) are the same. Figure 3 differs from the J/S monostatic equivalent circuit shown in Figure 4 in Section 4-7 in that the space loss from the jammer to the radar receiver is different.

Figure 3. Main Lobe Stand-Off / Stand-In ECM Equivalent Circuit

The equations are the same for both SOJ and SIJ. From the one way range equation in Section 4-3, and with inclusion of BF losses:

          [3]

From the two way range equation in Section 4.4:            [4]

so                   [5]

Note: Keep R and F in the same units. Converting to dB and using 10 log 4π = 10.99 dB:

     10 log J/S = 10 log P_j - 10 log [BW_j/BW_R] + 10 log G_ja - 10 log P_t - 10 log G_t - 10 log σ...         [6]

                        + 10.99 dB + 40 log R_Tx - 20 log R_Jx       

If the simplified radar equation is used, the free space loss from the SOJ/SIJ to the radar receiver is α_Jx, then equation [7] is the same as monostatic equation [6] in Section 4-7 except α_Jx replaces α, and the bandwidth reduction factor [BF] losses are included:

10 log J = 10 log P_j - BF + 10 log G_ja + 10 log G_r - α_Jx (factors in dB)          [7]

Since the free space loss from the radar to the target and return is the same both ways, α_Tx = α_Rx = α₁, equation [8] is the same as monostatic equation [7] in Section 4-7.

10 log S = 10 log P_t + 10 log G_t + 10 log G_r + G_σ - 2α₁ (factors in dB)            [8]

and    10 log J/S = 10 log P_j - BF + 10 log G_ja - α_Jx - 10 log P_t - 10 log G_t - G_σ + 2α₁ (factors in dB)   [9]

Notice that unlike equation [8] in Section 4-7, there are two different α's in [9] because the signal paths are different.

SIDE LOBE STAND-OFF / STAND-IN JAMMING

The equivalent circuit shown in Figure 4. It differs from Figure 3, (main lobe SOJ/SIJ) in that the radar

receiver antenna gain is different for the radar signal return and the jamming.

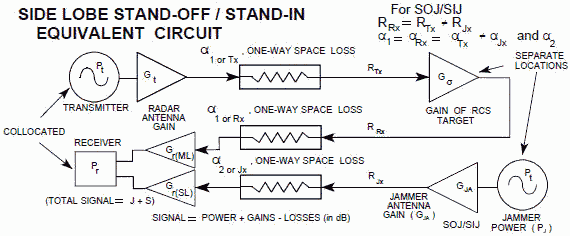
Figure 4. Side Lobe Stand-Off / Stand-In ECM Equivalent Circuit

To calculate side lobe jamming, the gain of the radar antenna's side lobes must be known or estimated. The gain of each side lobe will be different than the gain of the other side lobes. If the antenna is symmetrical, the first side lobe is the one on either side of the main lobe, the second side lobe is the next one on either side of the first side lobe, and so on. The side lobe gain is G_SLn , where the 'n' subscript denotes side lobe number: 1, 2, ..., n.

The signal is the same as main lobe equations [4] and [8], except G_r = G_r(ML)

          [10]

If simplified radar equations are used:

10 log S = 10 log P_t + 10 log G_t + 10 log G_r(ML) + G_σ - 2_α1 (factors in dB)

The jamming equation is the same as main lobe equations [3] and [7] except

 G_r = G_r(SL):        [11]

10 log J = 10 log P_j - BF + 10 log G_ja + 10 log G_r(SL) - α_Jx (factors in dB) [12]

so                 [13]

Note: keep R and F in same units. Converting to dB and using 10 log 4B = 10.99 dB:

   10 log J/S = 10 log P_j - BF + 10 log G_ja + 10 log G_r(SL) - 10 log P_t - 10 log G_t - 10 log G_r(ML) ...      [14]

                       - 10 log σ + 10.99 dB + 40 log R_Tx - 20 log R_Jx

(factors in dB)

If simplified radar equations are used:

     10 log J/S = 10 log P_j - BF + 10 log G_ja + 10 log G_r(SL) - α_Jx - 10 log P_t - 10 log G_t ...          [15]

                         - 10 log G_r(ML) - G_σ + 2_α1 (in dB)

Table of Contents for Electronics Warfare and Radar Engineering Handbook

Introduction | Abbreviations | Decibel | Duty Cycle | Doppler Shift | Radar Horizon / Line of Sight | Propagation Time / Resolution | Modulation | Transforms / Wavelets | Antenna Introduction / Basics | Polarization | Radiation Patterns | Frequency / Phase Effects of Antennas | Antenna Near Field | Radiation Hazards | Power Density | One-Way Radar Equation / RF Propagation | Two-Way Radar Equation (Monostatic) | Alternate Two-Way Radar Equation | Two-Way Radar Equation (Bistatic) | Jamming to Signal (J/S) Ratio - Constant Power [Saturated] Jamming | Support Jamming | Radar Cross Section (RCS) | Emission Control (EMCON) | RF Atmospheric Absorption / Ducting | Receiver Sensitivity / Noise | Receiver Types and Characteristics | General Radar Display Types | IFF - Identification - Friend or Foe | Receiver Tests | Signal Sorting Methods and Direction Finding | Voltage Standing Wave Ratio (VSWR) / Reflection Coefficient / Return Loss / Mismatch Loss | Microwave Coaxial Connectors | Power Dividers/Combiner and Directional Couplers | Attenuators / Filters / DC Blocks | Terminations / Dummy Loads | Circulators and Diplexers | Mixers and Frequency Discriminators | Detectors | Microwave Measurements | Microwave Waveguides and Coaxial Cable | Electro-Optics | Laser Safety | Mach Number and Airspeed vs. Altitude Mach Number | EMP/  Aircraft Dimensions | Data Busses | RS-232 Interface | RS-422 Balanced Voltage Interface | RS-485 Interface | IEEE-488 Interface Bus (HP-IB/GP-IB) | MIL-STD-1553 & 1773 Data Bus |

  This HTML version may be printed but not reproduced on websites.