Calculating Pi (π)

The concept of π as the ratio of a circle's circumference to its diameter has been recognized since antiquity (see my article entitled "Rationalizing Pi"). Early calculations of π were conducted using geometric and numerical methods long before modern computing tools. Around 1900 BC, the Babylonians approximated π as 3.125, while the Egyptians, as evidenced by the Rhind Papyrus, calculated a value of approximately 3.1605. The Greek mathematician Archimedes of Syracuse (287–212 BC) advanced these efforts by inscribing and circumscribing polygons around a circle, calculating their perimeters to determine bounds for π. His approximation, which placed π between 3.1408 and 3.1429, was remarkably precise for his era.

The discovery of mathematical series allowed for further refinement. The Madhava-Leibniz series, formulated by the Kerala mathematician Madhava around 1400 and independently discovered by James Gregory and Gottfried Leibniz, expressed π as an infinite series:

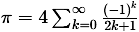
However, its slow convergence made it impractical for high-precision computations. In 1706, John Machin introduced an arctangent-based formula, allowing for faster convergence. His formula,

,

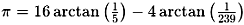became the foundation for many subsequent calculations.

By the 19th century, calculus enabled mathematicians to derive additional series for pan π. William Shanks, for instance, manually calculated π to 707 decimal places, though only 527 were correct. The advent of electronic computers revolutionized π-calculation methods. In 1949, the ENIAC computer computed π to 2,037 decimal places in 70 hours using Machin's formula. By 1958, the IBM 704 mainframe extended π to 10,000 places, and by 1987, Fujitsu's VP200 reached over a million digits using the Gauss-Legendre algorithm.

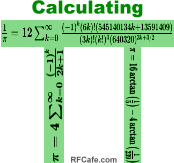
Today, the Chudnovsky algorithm, developed in 1988, dominates high-precision π calculations. This formula,

,

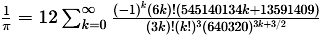converges exceptionally quickly, adding about 14 decimal places per term. It is paired with highly optimized arithmetic techniques, such as Fast Fourier Transform (FFT) multiplication, to handle the enormous numbers involved.

In 2021, a team at the University of Applied Sciences Graubünden in Switzerland used a high-performance computing cluster to compute 𝜋 π to 62.8 trillion decimal places. A year later, Japanese software engineer Emma Haruka Iwao used Google Cloud infrastructure to extend this to 100 trillion places. These calculations required months of processing and employed specialized tools such as Y-cruncher, which is designed for extreme precision in numerical computations.

For smaller-scale applications, π can also be computed programmatically. Below is an example of Excel VBA code for calculating π to a specified number of decimal places using the Leibniz formula:

Public Function CalculatePi(DecimalPlaces As Integer) As String
Dim k As Long
Dim pi As Double
Dim terms As Long
Dim sign As Double
Dim i As Long
Dim result As String
pi = 0
terms = DecimalPlaces * 100
sign = 1
For k = 0 To terms
   pi = pi + (sign / (2 * k + 1))
   sign = -sign
Next k
pi = pi * 4
result = Application.WorksheetFunction.Text(pi, "0." & String(DecimalPlaces, "0"))
CalculatePi = result
End Function

To use this code, open the VBA editor in Excel by pressing Alt + F11. Insert a new module and paste the code. Close the editor and return to Excel, where you can call the function in a cell, such as =CalculatePi(10), to calculate π to 10 decimal places. While this method illustrates the principle, it is not suitable for computing π to millions or trillions of digits, as modern computations require advanced algorithms and hardware.

This content was generated by the ChatGPT artificial intelligence (AI) engine. Some review was performed to help detect and correct any inaccuracies; however, you are encouraged to verify the information yourself if it will be used for critical applications. In some cases, multiple solicitations to ChatGPT were used to assimilate final content. Images and external hyperlinks have also been added occasionally. Courts have ruled that AI-generated content is not subject to copyright restrictions, but since I modify them, everything here is protected by RF Cafe copyright. Your use of this data implies an agreement to hold totally harmless Kirt Blattenberger, RF Cafe, and any and all of its assigns. Thank you. Here are the major categories.

Electronics & High Tech Companies | Electronics & Tech Publications | Electronics & Tech Pioneers | Electronics & Tech Principles | Tech Standards Groups & Industry Associations | Societal Influences on Technology
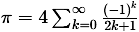
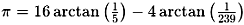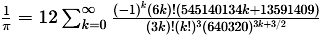